効果量とは何か？
研究や実験を行う際、統計的に有意な差が見られることは重要ですが、その差が実際にどれほどの「大きさ」や「意味」を持っているのかを知るために「効果量」が使用されます。
例えば、ある新しい勉強法Aが従来の勉強法Bよりもテストの成績を上げることが統計的に示されたとします。しかし、その上昇分が1点だけだった場合、実用的には大きな意味があるとは言えません。効果量はこの「1点の差」が実際にどれほどの意味を持つのかを示す指標となります。
具体例を交えての効果量
考えてみましょう。2つの異なるダイエット方法を比較した研究を想像してください。100人の参加者を2つのグループに分け、グループ1はダイエット方法A、グループ2はダイエット方法Bを試します。1ヶ月後、両グループの平均体重減少量を測定します。
結果、Aグループは平均で3kg、Bグループは平均で2.8kgの減少が見られました。統計的な検定を行うと、これは有意な差であると示されます。しかし、0.2kgの差が実際にどれほどの意味を持つのかを知るためには効果量を計算する必要があります。
Cohenのdを用いた効果量の計算
この例での、効果量をCohenのdを計算します。Cohenのdは以下の式で計算されます。
※ここでは対象群の標準偏差で代用しましたが、厳密には「SDpooled2つの群のプールされた標準偏差」を使うようです。このあとの、Rでのスクリプトの書き方では、「2つの群のプールされた標準偏差」を使う方法を示します。
この研究での標準偏差（ここでは対象群の標準偏差）を1kgとすると、Cohenのdは次のように計算されます。
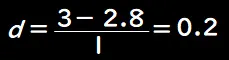
このdの値は「小」な効果であると解釈されます（一般的に、0.2は小、0.5は中、0.8は大とされます）。つまり、統計的に有意な差が見られたものの、実際の効果の大きさはそれほど大きくないことが示されました。
ここまでのまとめ
効果量は、単に統計的な差があるという情報だけではなく、その差が実際にどれほど実用的な意味を持つのかを示す重要な指標です。研究の結果を評価する際には、統計的有意性と効果量の両方を考慮することが必要です。
効果量はサンプル数によって変化することはありません。一方で、検定で使うp値はサンプル数を多くすれば、どんどん小さくなっていく性質があるのです。
したがって、有意差が出たとしても、それは本当に差があるという対立仮説が正しかったからなのか、それともサンプル数を無駄におおきくして無理やりにp値を小さくし有意差を出したものなのかは分からないので、最近の論文では同時に効果量を記載するように求められることが多くなっています。
参考文献
１）"Cohen, J. (1988). Statistical power analysis for the behavioral sciences (2nd ed.). Hillsdale, NJ: Lawrence Erlbaum Associates."
２）『英語教育研究』31 (2008), 57-66. 研究論文における効果量の報告のために
３） ISBN-13 : 978-4326250721
４） ISBN-13 : 978-4130420655
Rで効果量(cohen's d)を計算
Cohenのdの算出方法は以下のとおりです。（さきほどのように対象群の標準偏差で代用する場合もあります。）
2つの群のプールされた標準偏差は、2つの独立したサンプルの標準偏差を組み合わせたものです。これは、2つの群のデータが互いに似たような分散を持つ場合、特にt検定のような統計的手法を使用する際に役立ちます。具体的には、プールされた標準偏差は上の式で計算されます。
それでは実際にRで計算してみましょう。
score.csvファイルを読み込むところからスクリプトを開始します。
score.csvファイルは以下のデータが入っています。
Rスクリプトは以下のとおりです。
#csvファイルの読み込み
df <- read.csv("D:/ブログ用/17R/R#4 cohenD/score.csv")
#←ご自身のcsvファイルの場所を指定してくださいね。
# 2つのサンプルのデータ
group1 <- c(df$control) # グループ1のデータを抽出
group2 <- c(df$drug) # こちらにグループ2のデータを抽出
# プールされた標準偏差の計算
n1 <- length(group1)
n2 <- length(group2)
sd1 <- sd(group1)
sd2 <- sd(group2)
sdpooled <- sqrt(((n1 - 1) * sd1^2 + (n2 - 1) * sd2^2) / (n1 + n2 - 2))
# Cohenのdの計算
d <- abs((mean(group1) - mean(group2))) / sdpooled
print(d)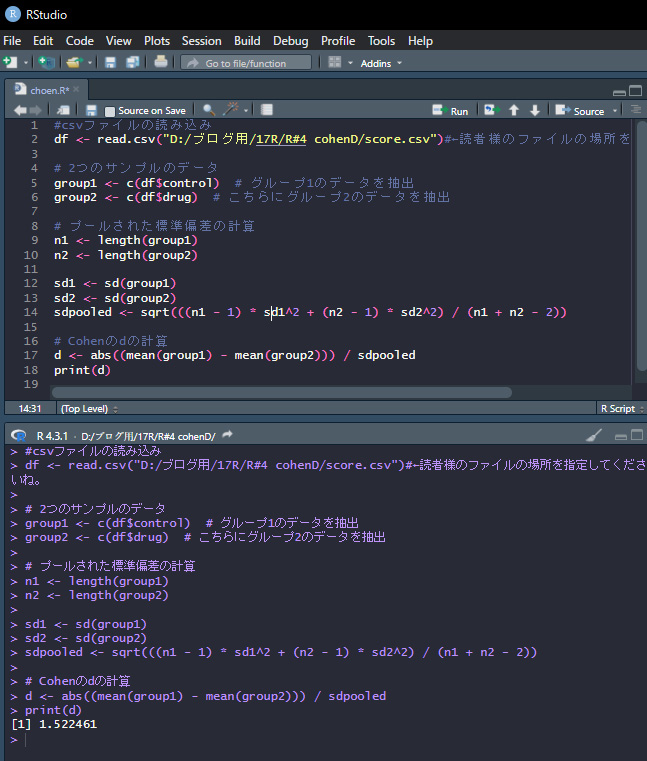
スクリプトを実行すると、上の写真のように、ｄ＝1.522461と出ました。
めでたしめでたし。
最後まで読んでいただきありがとうございました。