統計学はデータを分析し理解するための強力なツールです。その中でも、データの要約は非常に重要なステップです。データを要約することで、大量の情報を簡潔に表現し、パターンや傾向を見つけ出すのに役立ちます。
この記事では、データの要約方法に焦点を当て、平均、中央値、分散、標準偏差について詳しく説明します。
平均(Mean)
平均は、データセット内のすべての値の合計をその個数で割った値です。以下の式で表されます。
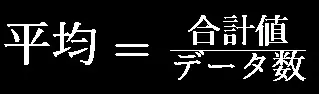
平均の特徴と重要性は以下の通りです:
- データの中心傾向を示すため、一般的な「中心」や「平均」の値として使われます。
- 外れ値(極端に大きいまたは小さい値)に敏感であり、外れ値がある場合、平均は外れ値の影響を受けやすいです。
- 平均は、データが間隔尺度(値の間隔に意味がある)または比例尺度(値の比較に意味がある)の場合に最も適しています。
- 平均は多くの統計的手法で使用され、データセットの特性を理解し、推論を行う際に中心的な役割を果たします。
例えば、クラス内の生徒の身長データを考えてみましょう。これらの身長を平均することで、クラスの平均身長が計算され、クラス全体の平均身長が把握されます。
平均は統計学やデータ分析において基本的であり、データセットの特性を理解し、意思決定を行うために広く使用される重要な統計的指標の一つです。
中央値(Median)
中央値は、データを小さい順に並べたときに中央に位置する値です。中央値は外れ値に対してロバスト(頑健)であり、データの中心傾向を表すのに適しています。
中央値は、データセット内の値を小さい順に並べたときに、ちょうど中央に位置する値です。つまり、データを小さい値から大きい値の順に並べた場合、中央にある値が中央値です。中央値はデータの中心傾向を示すための一つの方法であり、特にデータに外れ値(極端に大きいまたは小さい値)が含まれている場合、平均値に比べてロバスト(頑健)な指標として役立ちます。
中央値の計算方法は以下の通りです:
- データを小さい順にソートします。
- データの数が奇数の場合:データの中央に位置する値が中央値です。
- データの数が偶数の場合:中央に位置する2つの値の平均が中央値です。
中央値の特徴は以下の通りです:
- 外れ値に対して影響を受けにくいため、データが偏っている場合に有用です。
- データが順序尺度(順序があり、大小関係がわかるが、間隔尺度ではない)の場合にも適しています。
- 一般的に、中央値は平均値と異なる値を示すことがあり、データの分布に応じてどちらを使用するか選択する必要があります。
例えば、収入データの分析を考えてみましょう。この場合、外れ値(例: 非常に高収入の人)が平均値に大きな影響を与える可能性があるため、中央値を使用することでより正確な中心傾向を把握することができます。
中央値は統計学やデータ分析において非常に重要で、特にデータセットの特性を理解し、意思決定を行う際に利用されます。
最頻値とは
最頻値(Mode)は、統計学で使用される重要な中心傾向の指標の一つです。最頻値は、データセット内で最も頻繁に現れる値、つまり最も多くの回数出現する値を表します。データセット内で他の値よりもっとも頻繁に出現する値を見つけるために使用されます。
最頻値の特徴と重要性は以下の通りです:
-
カテゴリカルデータでの利用: 最頻値は主にカテゴリカルデータや離散的なデータに適用されます。例えば、色、動物の種類、アンケートの回答など、値がカテゴリで表されるデータに対して最頻値を計算できます。
-
データセット内の代表的な値: 最頻値は、データセット内の代表的な値の一つとして考えられます。平均や中央値と同様、データセットの特性を理解するために使用されます。
-
複数の最頻値が存在する場合: あるデータセットにおいて複数の値が同じ頻度で最も多く出現する場合、そのデータセットは「多重最頻値」を持っていると言います。多重最頻値が存在する場合、データセットはモードが複数存在することになります。
例えば、あるクラスの試験スコアが以下のようなデータセットを考えてみましょう。
このデータセットの最頻値は「78」と「85」の2つで、両方が同じ回数(3回ずつ)出現します。したがって、このデータセットは多重最頻値を持っています。
最頻値はカテゴリカルデータや離散データの分析において、特にデータ内の傾向や特性を理解するために役立ちます。ただし、連続的な数値データに対しては平均や中央値の方が一般的に使用されます。
分散(Variance)と標準偏差(Standard Deviation)
分散と標準偏差は、データのばらつきや散らばりを測定するための統計的指標です。これらの指標は、データの散らばりの程度を把握し、データセットの特性を理解するのに役立ちます。
分散(Variance)は、データセット内の各データポイントと平均値の差を二乗して合計した値の平均です。分散は以下の式で表されます。
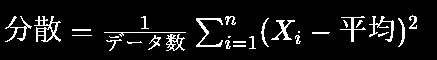
ここで、Xi は各データポイント、平均はデータセットの平均値、n はデータの総数です。
分散の特徴は以下のとおりです。
・各データポイントと平均値の差を二乗するため、外れ値があると分散は大きくなります。
・分散は平均からの距離を考慮するため、データの散らばりを定量的に評価します。
標準偏差(Standard Deviation)は分散の平方根で、分散と同様にデータの散らばりを示す指標です。標準偏差は以下の式で表されます:

標準偏差の特徴は以下の通りです:
・外れ値に対しても分散よりロバスト(頑健)であり、分散と比較して外れ値の影響を受けにくいです。
・標準偏差は正確な距離を示すため、データセットの散らばりを評価するのに有用です。
分散と標準偏差は、データの変動性や不確実性を理解し、データセットの特性を分析するのに役立ちます。特に、データ分布の形状や外れ値の有無を考慮する際に重要な指標となります。
まとめ
データの要約方法として、平均、中央値、分散、標準偏差は非常に重要です。
これらの指標を適切に使用することで、データの特性を理解し、意思決定や予測モデルの構築に役立ちます。
ただし、データの性質に応じて適切な要約方法を選択することが重要です。外れ値の影響を受けにくい中央値を使うか、分散と標準偏差を用いてデータのばらつきを評価するか、問題に合わせて選択しましょう。
統計学の基本を理解することは、データ駆動型の意思決定や問題解決において不可欠なスキルです。データの要約方法をマスターすることで、統計学の扉が開かれ、データの深い理解が可能になります。
参考文献
1) 統計学入門 (基礎統計学Ⅰ) 東京大学教養学部統計学教室 ISBN-13 : 978-4130420655

