広告 統計学基礎

「離散型確率分布とは？」ベルヌーイ、二項、幾何、ポアソン分布の解説

2023年9月29日

離散確率分布は、取り得る値が離散的（例: 整数）なランダムな変数の確率分布です。今日はその代表例について解説します。

ベルヌーイ分布

ベルヌーイ分布について知っていますか？複雑そうな名前ですが、実はとてもシンプルで理解しやすい分布なんです。

1. ベルヌーイ分布って何？

ベルヌーイ分布は、二つの結果しか出ない試行の確率分布を表すものです。例えば、コインを1回投げる場合、表が出るか裏が出るか、2つの結果しか考えられませんよね？このような場面で使われるのがベルヌーイ分布です。

2. 特徴をざっくりと

  • 二つの結果: 成功（例：コインの表）と失敗（例：コインの裏）の2つの結果しか出ません。
  • 確率は一定: 各試行で成功する確率は常に一定。コイン投げで言えば、公正なコインなら表が出る確率はいつも50%です。

3. 数式でみるベルヌーイ分布

ベルヌーイ分布は以下のように数式で表されます

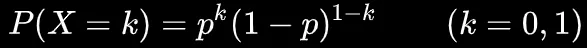
ここで、

は成功（1）か失敗（0）を示す変数

は0または1の値を取ります（0なら失敗、1なら成功）

は成功の確率

例えば、コインの表が出る確率を ｐ＝0.5とした場合、コインが表になる確率はこの式を使って計算できます。

4. まとめ

ベルヌーイ分布は、2つの結果しか出ないシンプルな試行の確率を扱う際に使用される分布です。日常生活の中で「成功 or 失敗」「Yes or No」のような二択の状況は多く、ベルヌーイ分布はそういった場面での確率を考える際の大事なツールとなります。

これからも統計学の旅を続けていく中で、ベルヌーイ分布の考え方は基礎として役立つこと間違いなし！しっかり理解して、次のトピックへのステップアップを目指しましょう。

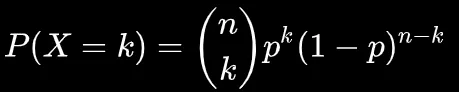
ここで、

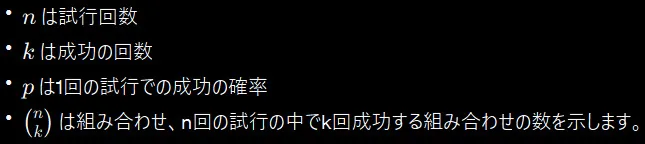
ここで、

例：公正なコインを10回投げたとき、表が3回出る確率は上の式を使って計算できます。

4. 二項分布の実用例

二項分布は、現実世界の多くの場面で役立ちます。製造ラインでの不良品の割合、アンケートの結果、クリニカルテストでの効果発現率など、成功・失敗の試行が繰り返される場面での確率を知りたいときに使用されます。

5. まとめ

二項分布は、ベルヌーイ分布を複数回繰り返した場合の成功回数の確率を表すもの。日常生活やビジネスの中で「何回中何回成功するか？」という問いは頻繁に出てくるため、二項分布の理解は非常に役立ちます。

幾何分布

何回目で初めて成功するか、そんな疑問を数学的に解明するのが幾何分布です！

1. 幾何分布って何？

幾何分布は、ベルヌーイ試行（成功 or 失敗の二つの結果しか出ない試行）を繰り返し行った際に、初めて成功するまでの試行回数の確率分布を示します。例えば、「公正なコインを投げ続けて、初めて表が出るのは何回目か？」という疑問に答えるのが幾何分布です。

2. 幾何分布の特徴

  • 独立な試行: 各試行は独立しており、一つの試行の結果が次の試行の結果に影響を与えることはありません。
  • 成功の確率は一定: どの試行でも成功する確率は同じです。

3. 数式で見る幾何分布

幾何分布は以下のような数式で表されます

ここで、

は初めて成功するまでの試行回数

は試行回数（1, 2, 3, ...）

は1回の試行での成功の確率

例：公正なコインを投げ続けて、初めて表が出るのが3回目である確率は、上の式を使って計算できます。

4. 幾何分布の実用例

幾何分布は、多くの現実的なシチュエーションでの応用が考えられます。例えば、新製品の宣伝を行って、初めての顧客が購入するまでの宣伝回数や、品質検査で初めて不良品が見つかるまでの検査回数など、初めての成功や発生を知りたい場面で使用されます。

5. まとめ

幾何分布は、繰り返し行われるベルヌーイ試行で初めて成功するまでの試行回数の確率を考える際に使用される分布です。日常生活やビジネスの中で「初めての成功はいつ？」という疑問は頻繁に出てくるため、幾何分布の理解は非常に役立ちます。

ポアソン分布

1. ポアソン分布とは？

ポアソン分布は、ある一定の期間や範囲で発生する平均的な出来事の数が与えられたとき、具体的に「k回」その出来事が発生する確率を示すものです。例えば、1時間あたり平均5回の来客がある店で、具体的に1時間に10人の客が来る確率を求めたいときに使用します。

2. 具体的なシチュエーション

  • 1日に平均10件のメールが届くメールボックスで、1日に20件のメールが届く確率は？
  • 平均毎月2回地震が起きる地域で、ある月に5回地震が起きる確率は？

上記のような場面でポアソン分布は役立ちます。

3. ポアソン分布の式

ポアソン分布の確率質量関数は以下のように表されます。

ここで、
は事象がk回発生する確率

は期待される発生回数（平均）

はネイピア数（約2.71828）

4. 特性

  1. 期待値と分散: ポアソン分布の期待値も分散も
     となります。
  2. レアイベント: ポアソン分布は、発生する確率が低い（レアな）事象に対して特に適しています。
  3. 独立性: 考えている期間や範囲内での事象の発生は独立している必要があります。

5. まとめ

ポアソン分布は、特定の期間や範囲での事象の発生回数に関する確率を扱う際に非常に役立つ分布です。統計学やデータ分析の現場で頻繁に使われるので、理解しておくと非常に有益です。

参考文献

１） 統計学入門 (基礎統計学Ⅰ)  東京大学教養学部統計学教室  ISBN-10：9784130420655
２） 統計解析がわかった!  涌井良幸 (著) 日本実業出版社 ISBN-10:453404464X

-統計学基礎
-