今日は「連続型確率分布」に焦点を当てて、その基本と代表的な例をご紹介します。確率分布は、データ解析や機械学習、さらには物理や経済など多岐にわたる分野で使用されている基本的な概念です。それでは、早速見ていきましょう。
1. 連続型確率分布とは?
まず、確率分布の基本を理解するために、データを考えます。例えば、ある都市の1日の最高気温を1年間分収集したとしましょう。この気温データは連続的な値を持つため、どの特定の気温が観測されるかの確率を考える時、連続型の確率分布を用います。
連続型確率分布は、その名の通り、連続的なデータに関する確率を扱う分布です。この分布は、確率密度関数(pdf: probability density function)で表され、この関数の下の領域の面積が確率を表します。
2. 代表的な連続型確率分布
以下に、代表的な連続型確率分布の例をいくつか紹介します。
2.1 正規分布(ガウス分布)
最も有名であり、多くの自然現象や実験データにおいて出現します。
ベルカーブの形をしており、平均値(μ)と標準偏差(σ)の2つのパラメータで特徴づけられます。
例: ある試験の得点分布、人々の身長の分布など。
2.2 指数分布
指数分布は、特定の事象が次に起こるまでの時間や距離をモデル化するのに適した確率分布です。主に信頼性工学やキューイング理論などの分野で利用されます。
1. 特徴
-
記憶のなさ: ある時間tまで事象が発生しなかったとしても、それ以後の事象の発生率に影響を与えない性質を持っています。これは、たとえば電球の寿命や電話の到着間隔など、過去の履歴が未来の予測に影響を及ぼさないような場合に適用されます。
-
単一のパラメータ λ (ラムダ): このパラメータは「平均的に1単位時間あたりに事象が何回発生するか」を示す率または強度として解釈されます。例えば、λ = 2の場合、1時間に平均2回の電話がかかってくると解釈できます。
2. 確率密度関数
指数分布の確率密度関数(pdf)は以下のように表されます。

3. 累積分布関数
指数分布の累積分布関数(CDF)は、以下の式で表されます。
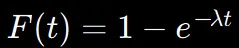
これは、時間tまでに事象が1回以上発生する確率を示します。
4. 平均と分散
指数分布の平均と分散は以下の通りです。

5. 用途
指数分布は、以下のような場面でよく用いられます。
- 機器の故障までの時間のモデリング
- サービスセンターに顧客が到着する間隔
- ネットワークのパケット到着時間
- 放射性物質の崩壊時間
6. まとめ
指数分布は、特定の事象が次に起こるまでの時間や距離をモデル化する際の非常に有用なツールです。その特性や性質を理解することで、さまざまな現実の現象やシステムを効果的に分析することができます。
まとめ
連続型確率分布は、統計学やデータ解析の基本的なツールとして非常に重要です。これらの分布を理解することで、データの背後にある構造やパターンを解釈しやすくなります。さまざまな分布を学ぶことで、実際のデータ分析の際にどの分布が適切かを選ぶ手助けとなります。
参考文献
1) 統計学入門 (基礎統計学Ⅰ) 東京大学教養学部統計学教室 ISBN-10:9784130420655
2)

