こんにちは!統計について学ぶ際、よく耳にする「信頼区間」。今回はこの信頼区間について、初心者向けにわかりやすく解説します。
信頼区間とは?
1. なぜ信頼区間が必要なのか?
統計データを取る際、一般には全ての個体や人々からデータを取ることは難しいので、一部をサンプルとして選び出して調査を行います。このサンプルデータを元に、全体の特性や挙動を予測するわけですが、サンプルはあくまで「一部」ですので、その結果が全体を正確に代表しているとは限りません。
信頼区間は、この不確実性を数値的に表現する方法として用いられます。具体的には、「真の値はこの範囲にある可能性が高い」という情報を提供してくれるのです。
2. 信頼区間の解釈
たとえば、「95%の信頼区間が[4.2, 4.8]である」という情報があった場合、これは「真の値がこの範囲に含まれる確率は95%である」と解釈します。しかし、注意点として、これは「95回のサンプリングのうち、約95回はこの範囲に真の値が含まれる」という意味であり、特定の1回のサンプリングで真の値がこの範囲に含まれる確率が95%であるとは言えません。
3. 信頼度と信頼区間の関係
信頼区間を計算する際に選ぶ「信頼度」(例: 95%)は、我々がどれだけその区間を信じるかの度合いを示しています。信頼度が高ければ高いほど、その区間が真の値を含む確率が高くなりますが、同時に信頼区間自体が広くなる傾向にあります。このため、研究の目的や状況に応じて適切な信頼度を選ぶことが重要です。
4. まとめ
信頼区間は、統計的な推定の不確実性を数値的に捉えるツールとして非常に役立ちます。統計的なデータ解析や研究の結果を理解し、適切に解釈するために、信頼区間の概念をしっかりと理解しておくことは非常に重要です。
信頼区間の計算方法
信頼区間の計算は、実際のデータ解析や研究の現場で頻繁に行われます。しかし、信頼区間を計算する背後の理論や方法は一見複雑に見えるかもしれません。ここでは、その詳細な計算方法をより深く探ってみましょう。
1. 前提条件
信頼区間を計算する前に、いくつかの前提条件が必要です。
データの分布: 信頼区間の計算は、しばしばデータが正規分布に従っているという前提のもとで行われます。特にサンプルサイズが小さい場合、この前提が非常に重要です。
サンプルサイズ: サンプルサイズが大きいほど、信頼区間は狭くなります。これは、大きなサンプルサイズの方が真の母集団の特性をより正確に推定できるためです。
2. 標準誤差
信頼区間の計算には「標準誤差」が必要です。標準誤差は、サンプル平均のばらつきを示す指標として用いられます。計算方法は以下の通りです。

2.3 z値とt値
前述の通り、信頼区間の計算にはz値が使用されます。しかし、サンプルサイズが小さい場合や母集団の標準偏差が未知の場合は、t分布を用いたt値が使われることもあります。t値はサンプルサイズと信頼度に応じて変わるため、t分布の表を参照する必要があります。
z-1. z値とは?
z値(またはzスコアとも呼ばれる)は、統計学における基本的な概念で、特に正規分布に関連して使用される値です。あるデータポイントが平均からどれだけ標準偏差の単位で離れているかを示す数値です。数式で表現すると以下のようになります。
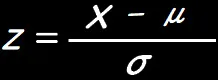
ここで、
は母集団の平均またはサンプルの平均
は母集団の標準偏差またはサンプルの標準偏差
z-2. z値の特徴
-
標準化: z値はデータを標準化するためのツールとして使用されます。z値を計算することで、異なる尺度や単位のデータを共通の尺度に変換することができます。
-
正規分布の下での位置: データが正規分布に従っている場合、z値はそのデータポイントが平均からどれだけ離れているかを示します。例えば、z値が1の場合、そのデータポイントは平均から1標準偏差だけ右側に位置していることを意味します。
-
確率の計算: z値を使用すると、正規分布テーブル(zテーブル)を参照して、特定のz値以下のデータが観測される確率を求めることができます。
z-3. 使用例
z値は、様々な統計的テストや手法、特に正規分布が関与する場面で使用されます。具体的には、母平均の検定、信頼区間の計算、異なるデータセット間の比較など、多岐にわたる分野で利用されています。
z-4. まとめ
z値は、あるデータポイントが平均値からどれだけ離れているかを標準偏差の単位で示す指標です。正規分布におけるデータの位置や分布の特性を理解する上で、非常に役立つツールとなっています。
t-1. t値とは?
t値は、統計学において重要な役割を果たす値で、特に小さなサンプルサイズを持つデータセットや、母集団の標準偏差が未知の場合に使用されることが多いです。t値は、t分布と密接に関連しています。
t値(またはtスコアとも呼ばれる)は、サンプル平均の位置と母平均の間の差を、標準誤差で正規化したものです。数式で表現すると以下のようになります。
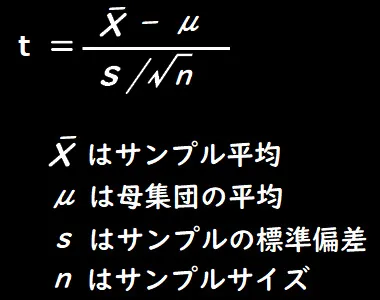
t-2. t値の特徴
-
t分布: t値はt分布に基づいています。t分布は正規分布に似ていますが、尾部がやや太くなっており、サンプルサイズが小さいときのデータの挙動をより正確に捉えることができます。
-
自由度: t分布は自由度というパラメータによって形状が変わります。自由度は、通常、サンプルサイズから1を引いた値()で計算されます。サンプルサイズが大きくなると、t分布は正規分布に近づきます。
-
確率の計算: t値を使用すると、t分布の表(tテーブル)を参照して、特定のt値以下のデータが観測される確率や、信頼区間などを求めることができます。
t-3. 使用例
t値は、統計的仮説検定(特に一樣のt検定や独立した二群のt検定など)において、サンプルの平均が母平均と有意に異なるかどうかを判断するために使用されます。また、回帰分析における各変数の係数の有意性を評価するためにも使用されます。
t-4. まとめ
t値は、サンプルの情報を元に母集団の特性や、サンプル間の差異を統計的に評価する際に非常に役立つ指標です。サンプルサイズが小さい場合や母集団の標準偏差が未知の場合に、特にその威力を発揮します。
2.4 信頼区間の計算式
先ほどの基本的な計算式を再掲します。
信頼区間=サンプル平均±(z値×標準誤差)
もしt値を用いる場合は、z値の部分をt値に置き換えます。
2.5 注意点
-
信頼区間は、あくまで推定の範囲を示すもので、真の母数がこの範囲に必ず含まれるわけではありません。
-
信頼区間の幅は、信頼度やサンプルサイズ、データのばらつきによって変わります。信頼度が高いほど、またサンプルサイズが小さい・データのばらつきが大きいほど、信頼区間は広くなります。
2.6 まとめ
信頼区間の計算は、統計的な不確実性を定量的に捉える手法として非常に有用です。しかし、その背後の理論や計算方法を理解することで、正確かつ適切な解釈が可能となります。

