こんにちは!今日は統計の中の一つのトピック、「単純線形回帰」について詳しく学ぶことにします。統計学が少し難しく感じるかもしれませんが、ここで一緒に基本的な概念と計算方法を学べば、もう少し身近に感じることができるでしょう。
1. 単回帰分析とは?
単回帰分析は、2つの変数間の関係を直線で表現するための統計的手法の一つです。一つの独立変数(説明変数)と一つの従属変数(目的変数)の関係を明らかにします。この関係を理解することで、一つの変数が変わると、もう一つの変数がどのように変動するのかを予測することができます。
具体例: アイスクリームの販売量と気温
夏の日、気温が上がると、アイスクリームの売り上げが増えることが予想されます。この場合、
- 独立変数(説明変数):気温
- 従属変数(目的変数):アイスクリームの販売量
となります。
気温が1度上がると、アイスクリームの販売量がどれだけ増加するのか、または逆に、ある日のアイスクリームの販売量からその日の気温を推測するのか、その関係を明らかにするのが単回帰分析です。
具体的なデータとして、以下のようなデータセットを考えてみましょう
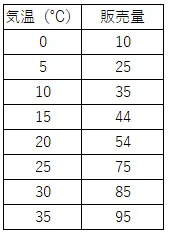
このデータを元に、気温とアイスクリームの販売量の間にどのような直線的な関係があるのかを調査します。単回帰分析を用いて、最も適切な直線をデータ上に引くと次のようになります。

単回帰分析は、このような具体的な状況での予測や分析に大変役立つ手法です。日常生活やビジネスの中で、2つの変数間の関係を知りたいと思ったとき、この単回帰分析を思い出してみてください。
2. 回帰直線の方程式
単回帰分析での目標は、データ間の関係を最もよく表現する直線を見つけることです。この直線を数式で表現すると、以下のような方程式になります。

ここで、

具体例: アイスクリームの販売量と気温
先ほどのアイスクリームの例を続けます。気温とアイスクリームの販売量の関係を直線で示したいと考えます。データを解析した結果、以下のような方程式を得たとします。
販売量=10+2.4×気温
この方程式では、
切片 β0 は10。これは気温が0℃のときのアイスクリームの予測販売量です(実際には0℃ではアイスクリームをたくさん売ることは難しいでしょうが、数学的なモデルとしての意味合いです)。
傾き β1は2.4。これは気温が1℃上昇すると、アイスクリームの販売量が2.4個増加することを示しています。
したがって、この方程式を用いれば、気温が25℃のときのアイスクリームの販売量を予測することができます。
0
このように、気温が25℃の日には約90個のアイスクリームが売れると予測できます。
直線の方程式は、データの関係性をシンプルかつ明確に示すツールです。具体的な数値を当てはめることで、未知の状況下でも予測を立てることができるのが、この方程式の強みです。
3. 傾きと切片の計算
単回帰分析の核心部分は、最も適切な直線をデータにフィットさせることです。この「最も適切な直線」とは、データポイントとの距離(実際のデータと予測される直線との間の差)が最小となる直線のことを指します。この距離を最小にする直線を求めるためには、傾き(β 1)と切片(β 0)を計算する必要があります。
傾きの計算傾き β1は、以下の式で計算されます。
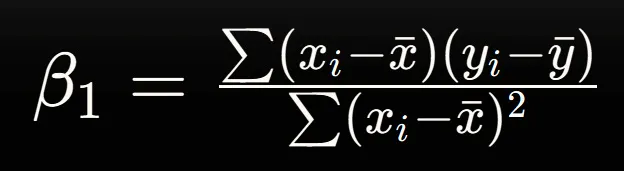
この式の中で、

この式は、データの変動(分散)と、独立変数と従属変数の共変動(共分散)の比として傾きを計算します。
切片の計算
切片 は、以下の式で計算されます。
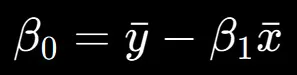
この式は、従属変数の平均値から、傾きと独立変数の平均値の積を引いたものです。この計算によって、y軸との交点である切片の値が得られます。
なぜこの計算方法なのか?
上記の計算方法は、データポイントと直線との差(誤差)の二乗和が最小となるように導かれたものです。これを「最小二乗法」と言います。この方法により、データの散布と直線との間の「フィット」が最も良いとされる直線を見つけることができます。
傾きと切片を計算することで、具体的な直線の方程式を得ることができます。この方程式を用いて、新しいデータに対する予測や、データの傾向を理解することができます。最小二乗法という考え方に基づいて、実際のデータに最も近い直線を引くことが、単回帰分析の目的となります。
4.まとめ
単回帰分析は、2つの変数間の直線的な関係を表現するための強力な手法です。この基本的な概念と計算方法を理解することで、実際のデータを使用して、2つの変数間の関係を評価することができます。次回は、実際のデータを用いて単回帰分析の計算を行う方法を学びましょう。

