こんにちは!統計やデータ分析に関心がある方、あるいは業務でのデータ解析が求められている方に、多重回帰分析についての基本をご紹介します。簡単な言葉で説明していきますので、安心して読み進めてくださいね。
1. 回帰分析って何?
まず、多重回帰分析を理解する前に、基本的な「回帰分析」とは何かを知ることが大切です。
回帰分析とは、変数間の関係性を数学的にモデル化する手法です。主に、1つの目的変数と1つ以上の予測変数の間の関係を調べるために使用されます。
例えば、家の価格(目的変数)が部屋の大きさ(予測変数)にどれくらい影響されるのかを知りたい場合、回帰分析を使用します。
2. そもそも「多重回帰分析」って?
多重回帰分析は、統計学の中で使われる手法の一つであり、目的変数の変動を2つ以上の予測変数を用いて説明する方法です。実際のデータ解析の場面での応用範囲は非常に広いです。以下、その特徴や仕組みを詳細に解説します。
基本概念と違い
線形回帰分析は、1つの予測変数と1つの目的変数との関係をモデル化するものでした。それに対して、多重回帰分析は複数の予測変数を取り入れることができます。これにより、目的変数に影響を与える複数の要因を同時に捉えることができるのが最大の特徴です。
どうして複数の要因を考慮するのか
現実の問題の中で、一つの出来事や現象が一つの要因だけで起こることは稀です。たとえば、商品の売上は広告費や製品の質、時期など多くの要因に影響されます。このような複数の要因を一度に考慮するために多重回帰分析が使われます。
調整という観点
複数の予測変数がある場合、予測変数間に相関が存在することがよくあります。例えば、広告費と商品の知名度は関連があるでしょう。多重回帰分析では、他の予測変数の影響を「調整」した上で、ある特定の予測変数が目的変数にどれだけの影響を持つかを評価します。これにより、各予測変数の「純粋な」影響を明確にすることができます。
数式で捉える多重回帰分析
多重回帰分析の数式は以下のように表されます。
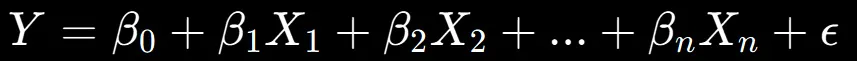
Yは目的変数、X1,X2,…は予測変数、β 0,β 1,…は各予測変数の影響度を示す係数で、ϵはモデルが捉えきれない誤差を示します。この数式の基盤の上で、データ分析が行われ、最適な係数が計算されることになります。
3. 多重回帰分析のメリット
多重回帰分析は、データ解析の分野で多くの研究や実務で使用されています。その理由は、多重回帰分析が持つ数々のメリットにあります。以下に、その主なメリットを詳しく解説します。
複数の要因を同時に評価
多重回帰分析の最大のメリットは、複数の予測変数を同時に考慮できる点です。現実の問題や現象は、多くの要因によって影響されるため、これを一つのモデルで捉えることができると、より現実に即した解析が可能になります。
各要因の相対的な寄与の把握
多重回帰分析では、各予測変数の係数を通じて、その要因が目的変数に与える影響の大きさや方向を定量的に評価することができます。これにより、最も影響力のある要因や、逆に影響力の小さい要因を明確にすることができるため、戦略や方針の決定に役立てることができます。
共線性の考慮
予測変数間に強い相関が存在する場合、これを共線性と呼びます。共線性は、回帰係数の不安定性や誤解釈を招く可能性がありますが、多重回帰分析ではこの共線性を評価し、適切に取り扱うことができるため、より確かな分析結果を得ることができます。
交互作用の検討
二つの予測変数が組み合わさった効果、つまり交互作用を考慮することができます。これにより、ある変数の効果が他の変数のレベルによって変わる場面など、より複雑な関係性をモデル化することができます。
調整変数の導入
分析において、特定の変数の影響を調整したい場合、その変数を調整変数としてモデルに組み入れることで、他の主要な予測変数の純粋な効果を評価することができます。これは、因果関係の推定や外部要因の影響を除去する際に非常に役立ちます。
4. しかし、注意点も…
多重回帰分析は多くのメリットを持つ一方で、その適切な利用のために考慮すべきいくつかの注意点が存在します。これらの点を理解し、適切に取り扱うことで、より信頼性の高い分析結果を得ることができます。
共線性の問題
既に触れた共線性ですが、予測変数間の強い相関は、回帰係数の推定を不安定にする可能性があります。これにより、実際の影響よりも大きくまたは小さく推定されることや、統計的に有意ではないと誤って判断されるリスクがあります。共線性の確認や、必要に応じて変数の選択や変換を行うことが重要です。
過学習のリスク
あまりにも多くの予測変数をモデルに取り入れると、過学習(overfitting)のリスクが高まります。これは、モデルが学習データのノイズまで学習してしまい、新しいデータに対する予測性能が低下する現象を指します。変数の選択やモデルの複雑さに注意を払うことで、過学習のリスクを抑制することができます。
因果関係の誤解
多重回帰分析によって関連が見られるからといって、それが因果関係を意味するわけではありません。相関関係と因果関係は異なるため、因果関係を主張する際には十分な根拠や外部的な情報をもとに慎重な判断が求められます。
残差の正規性や等分散性
多重回帰分析の基本的な前提として、残差(実測値と予測値の差)の正規性や等分散性があります。これらの前提が満たされない場合、回帰係数の推定や有意性検定が不正確となる可能性があるため、残差の分布や形状を適切に確認し、必要に応じてモデルの修正や変数の変換を行うことが重要です。
5. まとめ
多重回帰分析は、複数の要因を考慮したデータ分析を行うための強力な手法です。ただし、その適用には注意が必要です。初学者の方は、まずは基本的な理解から始め、徐々に複雑な分析に挑戦してみることをおすすめします。

