皆さん、こんにちは!統計学の世界では、データに隠された真実を見つける作業をしますが、その道中で「過誤」という2つの罠が常に私たちを待ち受けています。今日は、この統計学における「第一種の過誤」と「第二種の過誤」について、具体例を交えながら、理解しやすいように解説します。
まず、統計学における過誤とは何かを知ることから始めましょう。過誤とは、統計的な推論において、誤った結論を出してしまうことです。特に、仮説検定という手法を用いる際に、2種類の過誤に注意が必要です。
第一種の過誤とは?
第一種の過誤(Type I error)は、「偽陽性(False Positive)」とも呼ばれ、実際には正しい帰無仮説を誤って棄却してしまう誤りのことを指します。これは、無実の人に有罪の判決を下してしまうことに例えられます。
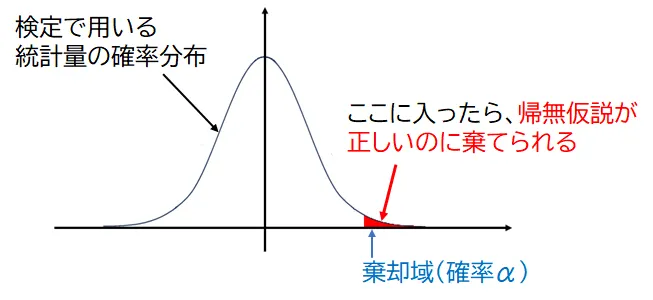
帰無仮説が棄却されるのは、標本調査の結果が「棄却域」に入ったときです。
棄却域に入る確率αのことを「有意水準」と呼びます。
つまり、帰無仮説が本当であったとしても、偶然のばらつきによって標本調査の結果が棄却域に入ることがあり、その確率はαになります。
そのため、「第一種の過誤を犯す確率」は、有意水準αと等しいと考えられます。これは通常、検定前に設定します(例: 5%や1%など)。
第二種の過誤とは?

一方で、**第二種の過誤(Type II error)は、「偽陰性(False Negative)」とも呼ばれ、実際には偽である帰無仮説を誤って棄却しない誤りのことを指します。これは、本来は有罪である犯人を誤って無罪放免にしてしまう状況にたとえることができます。第二種の過誤を犯す確率はβ(ベータ)と表され、しばしば検出力(1−β)**を考慮して、検定の設計がなされます。
第一種と第二種の過誤のバランス
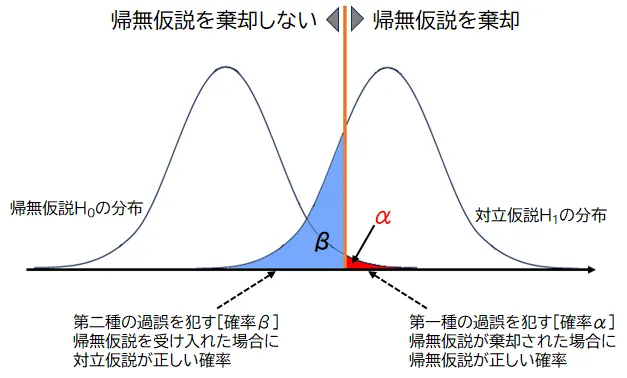
統計的な検定を行う際には、第一種の過誤と第二種の過誤のバランスを考慮する必要があります。第一種の過誤のリスク(α)を小さくすると、一般に第二種の過誤のリスク(β)が大きくなる傾向があります。 これは逆もまた真であり、βを減らすためにはαを増やす必要がある場合があります。 研究者は、実験や分析の目的に応じて、これらのリスクを適切に調整する必要があります。
第一種と第二種の過誤をコントロールする方法
第一種の過誤(偽陽性)と第二種の過誤(偽陰性)のリスクは、互いにトレードオフの関係にあります。一方を減らせば、他方が増える傾向にあるため、両者のバランスを考慮することが重要です。ここで、過誤をコントロールするための主要な方法をいくつか紹介します。
1. サンプルサイズの調整
サンプルサイズ(標本の大きさ)は、過誤のリスクに直接影響を与えます。一般的に、サンプルサイズを大きくすることで、第二種の過誤のリスクを減らすことができます。しかし、あまりにも大きなサンプルサイズは、第一種の過誤を犯しやすくする可能性もあるため、慎重にサイズを選ぶ必要があります。
2. 有意水準の設定
有意水準(通常、αとして表される)を設定することは、第一種の過誤をコントロールするための一般的な方法です。有意水準を低く設定すればするほど、誤って帰無仮説を棄却するリスクを低減できます。しかし、この設定を厳しくしすぎると、実際に効果がある場合にそれを見逃すリスク、つまり第二種の過誤が高まる可能性があります。
3. 検出力の分析
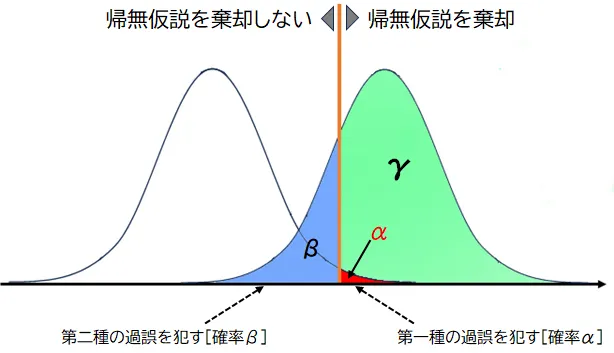
検出力(上図のγの部分。通常、1-βとして表される)は、実際に効果があるときにその効果を検出できる確率です。検出力を高めることは、第二種の過誤を減らすために重要です。検出力分析を事前に行い、適切なサンプルサイズやテストの設計を計画することが、この過誤を減らす鍵となります。
4. テストの選択
使用する統計的テストの種類によっても、過誤のリスクは変わります。例えば、一方向性テストは二方向性テストよりも第一種の過誤のリスクを低く保つ傾向があります。研究の仮説に最も適したテストを選択することが重要です。
5. ボンフェローニ修正などの手法
複数の比較を行う場合、第一種の過誤の総リスクをコントロールするためにボンフェローニ修正のような手法を適用することがあります。これは、有意水準を複数の比較の数で割ることにより、誤った結論を出す全体的なリスクを抑える方法です。
小まとめ
過誤を完全に排除することは不可能ですが、上記のような戦略を用いることで、そのリスクを管理し、より信頼性の高い結果を得ることができます。統計的推論においては、どの程度のリスクが許容可能かを判断し、その上で最適な戦略を選択する知識が必要です。
統計手法と過誤の関係性
統計手法を選ぶ際には、それぞれの手法が持つ特性と、テストしたい仮説の性質を考慮する必要があります。手法によっては、第一種または第二種の過誤のリスクを高めることもあります。以下に、よく使われる統計手法と過誤の関係性についていくつかの例を挙げます。
1. T検定
T検定は、二つの平均値の違いが統計的に有意かどうかを評価するためによく用いられます。このテストは、データが正規分布に従っているという前提に基づいています。この前提が妥当でない場合、第一種の過誤のリスクが高まる可能性があります。
2. ANOVA(分散分析)
ANOVAは、三つ以上のグループ間で平均値に差があるかどうかを検証する手法です。ANOVAは、複数の比較を同時に行うことができ、過誤のリスクをコントロールするために、事前に設定された全体的な有意水準を維持します。ただし、グループ間の分散が大きく異なる場合、第二種の過誤を犯すリスクが高くなることがあります。
3. 回帰分析
回帰分析は、変数間の関係をモデル化します。適切なモデル仮定と変数選択がなされた場合、有用な結果をもたらすことが多いです。しかし、モデルが過剰に複雑だと、データに存在しないパターンを見つけ出す(つまり第一種の過誤)リスクがあります。
4. ベイズ統計
ベイズ統計は、事前情報を取り入れることができ、更新されたデータに基づいて仮説の確からしさを評価します。ベイズアプローチは、データが限られている場合や、事前情報が有用な場合に、第二種の過誤を減らすのに役立つことがあります。
手法選択のポイント
適切な手法を選ぶ際のポイントは以下の通りです。
- データの特性: データが持つ分布や、サンプルサイズなど、データの特性を理解することが重要です。
- 仮説の性質: 何を証明しようとしているのか、どのような仮説を立てているのかを明確にします。
- 手法の前提条件: 各統計手法が持つ前提条件を確認し、それらがデータと合致しているかを評価します。
統計的手法の選択は、研究デザインの初期段階で慎重に行うべきです。その選択が結果の解釈に直結し、研究の信頼性を左右するからです。データを深く理解し、目的に応じた適切な統計手法を選ぶことで、第一種および第二種の過誤を適切に管理し、より真実に近い結論を導くことができるでしょう。
実践で学ぶ - 統計的仮説検定の手法と過誤の管理
ケーススタディ: 新薬の効果検証
ある製薬会社が、新しいインフルエンザ治療薬の効果を評価するための臨床試験を行っています。我々の目標は、この新薬が従来の治療法と比較して有意に効果があるかどうかを検証することです。
ステップ1: 仮説の設定
- 帰無仮説(H0): 新薬の効果は従来の治療法と同じである。
- 対立仮説(H1): 新薬の効果は従来の治療法と異なる。
ステップ2: 適切な統計手法の選択
この場合、二つの独立したサンプル(新薬を使用したグループと従来の治療法を使用したグループ)の平均効果を比較する必要があります。データが正規分布していると仮定できる場合、独立サンプルt検定を使用するのが適切です。
ステップ3: データ収集と検定
試験結果から得られたデータを用いてt検定を実施します。ここで、有意水準(α)を5%に設定することで、第一種の過誤を犯すリスクを管理します。
ステップ4: 結果の解釈
t検定の結果、p値が0.04であったとします。これは、帰無仮説を棄却し、新薬が従来の治療法と統計的に有意に異なる効果があると結論付けることができることを意味します。ただし、5%のリスクで第一種の過誤を犯している可能性があることも意識しておく必要があります。
過誤の管理
このケーススタディでは、第一種の過誤をコントロールするために有意水準を設定しました。しかし、第二種の過誤についても注意が必要です。たとえば、新薬の効果が非常に微妙であり、サンプルサイズが小さすぎる場合、この違いを見落としてしまうかもしれません。これを避けるためには、事前にパワーアナリシスを行って十分なサンプルサイズを確保することが重要です。
小まとめ
このケーススタディを通じて、統計的仮説検定の基本的なステップを見てきました。適切な手法の選択、正確なデータの収集、そして過誤の管理は、信頼できる結論に至るための鍵です。統計学はデータに隠された真実を明らかにするための強力なツールであり、それを最大限に活用するためには、慎重な計画と理解が必要です。
結果の伝え方

結果報告の重要性
統計的な結果は、数字の羅列で終わらせるのではなく、その意味を明確に伝える必要があります。研究結果が持つ意義を関係者に理解してもらうためには、統計用語を適切に使い、結果の解釈を正しく行うことが欠かせません。
ステップ1: 結果の提示
統計的検定の結果を伝える際には、以下の点を含めるべきです。
- p値とその意味
- 効果量(effect size)とその重要性
- 信頼区間の提示
- 第一種及び第二種の過誤の可能性についての説明
これらの要素は結果の信頼性を評価し、研究の文脈で結果を解釈するのに役立ちます。
ステップ2: 解釈の提供
統計的な意義は実践的な意義とは異なる場合があります。p値が統計的に有意であっても、効果が小さい、あるいは臨床的に重要でない可能性があります。結果の解釈では、実際の応用において結果がどのような影響を持つかを評価する必要があります。
ステップ3: 文脈への配置
研究結果は常に関連する文脈の中で伝えるべきです。これには、既存の研究や理論との関係、および結果が持つ潜在的な影響が含まれます。視聴者が結果を独立した事象としてではなく、より広い領域の知識の一部として理解できるようにすることが大切です。
コミュニケーションのベストプラクティス
結果を伝える際には、以下のベストプラクティスを心がけましょう。
- 明瞭性: 専門用語の使用を最小限にし、可能な限り平易な言葉で結果を説明します。
- 透明性: 分析の過程をオープンにし、どのような選択がなされたかを明らかにします。
- 公平性: すべての結果を公平に扱い、都合の良いものだけを選んで報告しないようにします。
- 教育的アプローチ: 聞き手が統計に詳しくない場合は、結果が何を意味するのかを理解できるように教育的なアプローチを取ります。
小まとめ
統計的結果のコミュニケーションは、単に数値を伝える以上のものです。それは、研究の意味と価値を聞き手に伝え、彼らが情報を使って賢明な決断を下せるようにするプロセスです。
フィードバックを統計に活かす - 継続的改善のためのアプローチ
統計的分析は、その結果をどのように伝えるかだけでなく、受け取ったフィードバックをどのように活用するかにも大きく依存します。前回は、結果を伝えるベストプラクティスについて説明しましたが、今回は読者や関係者からのフィードバックを統計的分析にどのように統合するかを探ります。
フィードバックの重要性
読者やピアレビューからのフィードバックは、研究をより豊かで信頼性のあるものにする機会を提供します。批判的な意見は分析を強化し、潜在的な弱点や見落としがある場合はそれを明らかにすることができます。このような対話は、研究の品質を向上させるための不可欠なプロセスです。
ステップ1: フィードバックの評価
受け取ったすべてのフィードバックを公正に評価します。どのコメントが分析の精度を向上させるのに有益かを判断し、それに基づいて必要な変更を特定します。
ステップ2: 再分析
重要なフィードバックに対応して分析を再実施することが時には必要です。これには、異なる統計モデルを使用する、追加のデータを含める、あるいは異なる統計的手法を試すことが含まれます。
ステップ3: 結果の更新
再分析の結果に基づいて、結論や解釈を更新します。この過程では、新たな発見を透明に報告し、初期の分析とどのように異なるかを明確にすることが大切です。
フィードバックを取り入れるベストプラクティス
- 対話を促進する: フィードバックは対話から生まれるため、読者がコメントや質問をしやすい環境を整えることが重要です。
- 柔軟性を保つ: 新たな情報に基づいて、分析や解釈を変更する柔軟性を持つことが求められます。
- 継続的学習: 統計学は進化し続ける分野であるため、最新の手法や理論を学び続けることが重要です。
- ドキュメンテーション: 変更点や分析の更新を記録し、その理由と結果を文書化します。
小まとめ
フィードバックを統計的分析に統合することは、研究プロセスの透明性を保ち、結果の信頼性を高めるために不可欠です。継続的な改善は、より正確な知識を構築し、実世界での意思決定をサポートするためのキーとなります。読者からのフィードバックは研究を深め、より豊かな議論を生むための貴重な財産です。

