データの可視化は、情報を一目で理解しやすくするための強力なツールです。特に大量のデータを扱う現代において、適切な可視化方法を知っていると、データの傾向や特性を迅速に把握することができます。この記事では、主にヒストグラム、散布図、箱ひげ図の3つの可視化方法に焦点を当てて説明します。
ヒストグラム
データ分析の世界では、データの性質や分布を理解するためのさまざまな手法が存在しますが、その中でも「ヒストグラム」は、情報を直感的に捉えるための非常に強力なツールとして知られています。今回は、ヒストグラムの基本から、その魅力や活用方法について詳しく解説していきます。
1. ヒストグラムとは?
ヒストグラムは、データの分布を視覚的に示すグラフの一種です。データセットの各値の頻度や回数を縦軸に、データの範囲や区間を横軸に表示します。
2. ヒストグラムの特徴
- データの分布を把握: ヒストグラムを見るだけで、データの中心的な値や、どのような値が多いのか、外れ値はあるのかなどの情報を素早く把握することができます。
- 外れ値の発見: ヒストグラムにはデータの偏りや外れ値が一目瞭然となります。これにより、データの異常な部分や特異な特性を発見できます。
- 簡潔な可視化: データの大雑把な形状や傾向を簡潔に表現することができます。
3. ヒストグラムの活用方法
- 品質管理: 製造工程での不良品の発生頻度や、特定のサイズの製品がどれだけの頻度で製造されるかなどを把握するために使用されます。
- 市場調査: 顧客の年齢分布や購入金額の分布など、市場の特性を理解するために活用されます。
- 学術研究: 研究データの分布や特性を明らかにするための初歩的な分析手法として使用されることが多いです。
4. 注意点
ヒストグラムを解釈する際には、ビンのサイズ(各棒の幅)やビンの数に注意が必要です。これらの設定によって、ヒストグラムの形状が大きく変わることがあります。適切なビンの設定を行うことで、データの真の特性をより正確に捉えることができます。
まとめ
ヒストグラムは、データの分布や特性を迅速に把握するためのシンプルかつ強力なツールです。データ分析の初歩として、また、データの全体像を理解する際の基盤として、ヒストグラムの活用を心がけましょう。
散布図
データの解析や可視化には様々な方法がありますが、特に2つの変数間の関係性を視覚的に理解したい場合、散布図は欠かせないツールです。今回の記事では、散布図の基本的な特徴からその活用法までを掘り下げていきます。
1. 散布図とは?
散布図は、2つの変数の関係性を点としてプロットしたグラフのことを指します。横軸と縦軸にそれぞれ異なる変数をとり、データポイントを点として表示することで、2つの変数間の関係を視覚的に捉えることができます。
2. 散布図の特徴
- 相関の把握: 2つの変数がどれほど関連しているのか、または関連がないのかを瞬時に理解することができます。
- データの分布: データがどのように分布しているのか、クラスタや外れ値の存在を確認することができます。
- 直感的な可視化: 2つの変数間の関係を直感的に掴みやすく、非技術的な人々にも理解しやすい形で情報を伝えることができます。
3. 散布図の活用方法
- ビジネス: 売上と広告費の関係、製品の価格と売上数の関係など、2つの変数の関係性を調査する際に用いられます。
- 科学研究: ある変数がもう一つの変数にどれだけ影響を与えるのかを調査するための実験や観測結果をプロットするのに使用されます。
- 健康: 体重と血圧、運動量と体脂肪率など、2つの健康指標間の関係性を分析するために使用されることがあります。
4. 注意点
散布図は2つの変数間の関係を示すのが得意ですが、それ以上の多変数の関係性を示すのは難しいです。また、2つの変数が強い相関関係にあるとしても、それが因果関係を意味するわけではありません。相関関係と因果関係は異なる概念であることを理解し、適切に解釈することが重要です。
まとめ
散布図は、2つの変数の関係性を可視化する強力なツールです。ビジネスから学術研究まで幅広い分野で活用されています。データ分析の際には、散布図を駆使して、データの背後に隠れた情報やパターンを発見しましょう。
箱ひげ図
データの可視化には様々な方法が存在しますが、データの分布やばらつきを一目で理解するための効果的なツールとして「箱ひげ図」があります。この記事では、箱ひげ図の特徴、その解釈方法、そしてその活用のポイントについて詳しくご紹介します。
1. 箱ひげ図とは?
箱ひげ図(ボックスプロットとも呼ばれる)は、データの五数要約(最小値、第1四分位数、中央値、第3四分位数、最大値)を用いて、データの分布を表現するグラフです。
2. 箱ひげ図の構成要素
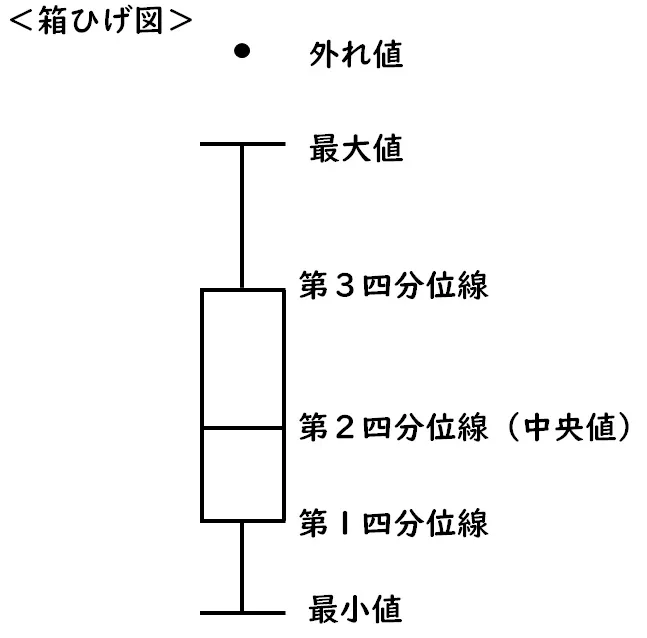
- 箱: 中央の箱は、第1四分位数(Q1)から第3四分位数(Q3)までのデータの範囲を表し、データの中央50%を示します。
- 中央線: 箱の中に引かれた線は、中央値(メディアン)を示します。
- ひげ: 箱の上下に伸びる線は、「ひげ」と呼ばれ、データの全範囲を示すものですが、外れ値を除外した範囲となります。
- 外れ値: ひげの外にプロットされる点は「外れ値」として表示され、通常の範囲から大きく外れたデータポイントを示します。
3. 箱ひげ図の活用方法
- データのばらつきの比較: 複数のグループやカテゴリー間でのデータのばらつきや中央値を比較する際に有効です。
- 外れ値の確認: 箱ひげ図を用いると、データに異常値や外れ値が存在するかすぐに確認できます。
- データの分布の理解: データがどのように分布しているのか、中心的な傾向や分布の幅を素早く把握することができます。
4. 注意点
箱ひげ図はデータの分布の大まかな形状を示すのが得意ですが、データの具体的な頻度や個々のデータポイントの詳細まで知ることはできません。そのため、箱ひげ図と他のグラフ(ヒストグラムや散布図など)を組み合わせて使用することで、より深いデータの理解が得られます。
まとめ
箱ひげ図は、データの分布やばらつきを手軽に可視化するための有効なツールです。正しく解釈し、適切な場面で活用することで、データ分析の幅がさらに広がります。

