数学や物理、経済学、機械学習の分野では、「偏微分」という概念が頻繁に登場します。
例えば、以下のような場面で偏微分が活用されます。
✅ 物理学:物体の運動を記述する方程式(速度や加速度)を導く
✅ 経済学:利潤最大化やコスト最小化の最適化問題を解く
✅ 機械学習:ニューラルネットワークの学習アルゴリズム(勾配降下法)に利用
では、偏微分とは何なのか?どのように計算すればよいのか?
本記事では、偏微分の基礎から応用までを詳しく解説 していきます!
1. 偏微分の基礎知識
1-1 偏微分とは?微分との違い
通常の微分(全微分)は、関数の変数を1つとし、その変数の変化に対する関数の変化率を求めるものです。
例えば、関数 f(x)=x2 の微分は
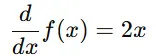
となります。
一方で、偏微分(partial differentiation) は、2つ以上の変数を持つ関数について、一つの変数のみを変化させた場合の変化率 を求める手法です。
例えば、関数
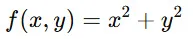
について、x だけを変化させた場合の変化率(偏微分) は、
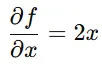
となります。(このとき、y は定数として扱います。)
1-2 偏微分の直感的なイメージ(図解)
偏微分の概念を直感的に理解するために、山の地形を考えてみましょう。

つまり、偏微分は特定の方向の変化を捉える数学的な道具 だと考えることができます。
1-3 偏微分の数学的定義
偏微分の定義は、一変数関数の微分と類似しています。
ある関数 f(x,y)の x に関する偏微分は、以下のように定義されます。
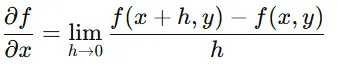
この式は、「y を固定したまま、x の小さな変化に対する関数の変化率を求める」ことを意味しています。
同様に、 に関する偏微分は、
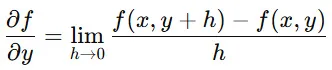
となります。
2. 偏微分の計算方法と例題
2-1 一変数関数の微分との比較
まず、一変数関数の通常の微分を復習しましょう。
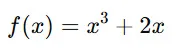
この場合、x の微分は
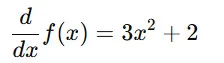
となります。
これに対し、多変数関数 f(x,y) の偏微分では、片方の変数を定数とみなして微分を行う ことがポイントです。
2-2 偏微分の基本的な計算ルール
✅ 関数 f(x,y)=x2+y2 の偏微分
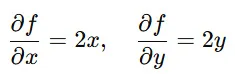
✅ 指数関数を含む偏微分
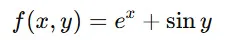
この場合、
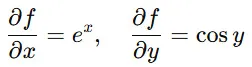
✅ 積の微分を含む偏微分
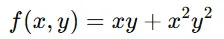
この場合、
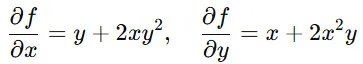

3. 偏微分の応用と実生活での活用事例
偏微分は、数学の理論だけでなく、物理学・経済学・機械学習 などさまざまな分野で活用されています。本章では、それぞれの応用事例について詳しく解説します。
3-1 物理学(速度・加速度の解析)
物理学では、偏微分を用いて運動方程式や波動方程式を記述 することができます。
① 速度と加速度の解析
例えば、物体の位置を時間 t と空間座標 x,y,z の関数として表す場合、
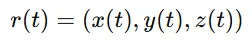
と書けます。
✅ 速度ベクトル
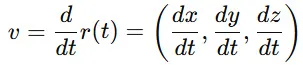
✅ 加速度ベクトル
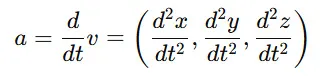
これは通常の微分ですが、風の流れや電磁場のように 複数の変数(空間座標 x, y, z と時間 t)を持つ関数 の場合、偏微分を用います。
② 波動方程式と偏微分
例えば、波の伝播を表す波動方程式 は、偏微分を使って記述されます。
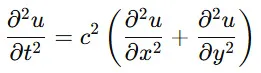
ここで、u(x,y,t)u(x, y, t) は時間と空間における波の振幅、cc は波の速さを表します。
📌 この方程式は、音の波、光の波、水の波などに適用される基本的な数式!
3-2 経済学(最適化問題と利潤最大化)
経済学では、偏微分を用いて利潤最大化や費用最小化 などの最適化問題を解きます。
① 企業の利潤最大化
企業の利潤(利益)を関数として表すと、
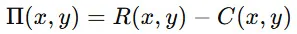
ここで、
- R(x,y) は売上(Revenue)
- C(x,y) はコスト(Cost)
- x,y は生産量や価格などの変数
利潤を最大化するためには、偏微分を用いて最適な x,y の値を求める 必要があります。
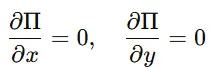
この方程式を解くことで、企業の最適な生産量や価格を決定できます。
② 需要と供給の分析
経済のモデルでは、消費者の行動を偏微分を用いて表現できます。例えば、価格弾力性 は、
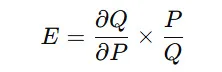
ここで、
- Q は需要量(Quantity)
- P は価格(Price)
📌 偏微分を使うことで、価格が変化したときにどの程度需要が変化するかを測定できる!
3-3 機械学習(誤差関数と勾配降下法)
機械学習では、モデルの最適化に偏微分が頻繁に使われます。特に、ニューラルネットワークの学習では、誤差関数を最小化するために勾配降下法を適用 します。
① 誤差関数の偏微分
例えば、回帰モデルの誤差関数(損失関数)を
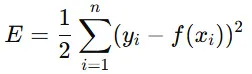
と定義すると、最適なパラメータを求めるために、
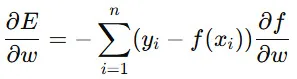
を計算しなければなりません。
② 勾配降下法(Gradient Descent)
ニューラルネットワークの学習では、偏微分を使って誤差を最小化する方向にパラメータを更新 します。
更新式は次のように表されます。
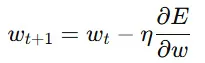
ここで、
- ww は重みパラメータ
- η\eta は学習率(Learning Rate)
- ∂E∂w\frac{\partial E}{\partial w} は誤差関数の偏微分(勾配)
📌 偏微分を計算し、学習率をかけてパラメータを調整することで、最適なモデルを学習できる!
4. Q&A(よくある質問)
Q1. 偏微分と全微分の違いは?
A. 偏微分は 一つの変数のみを変化させたときの変化率 を求めるもの。
全微分は すべての変数の影響を考慮して関数の変化を求めるもの。
Q2. 偏微分はどんな場面で役に立つの?
A. 偏微分は、
- 物理学:運動方程式、波動方程式
- 経済学:最適化問題、価格弾力性
- 機械学習:誤差関数の最適化
など、さまざまな分野で使われています!
Q3. 偏微分の計算が苦手!コツは?
A. 計算のコツは、
✅ 偏微分を求める変数以外は定数とみなす
✅ 基本的な微分ルール(積の微分・指数関数の微分)をマスターする
✅ 具体的な例題を解いて慣れる
5. まとめ
本記事では、偏微分の基礎から応用までを詳しく解説 しました。
✅ 偏微分のポイント
- 多変数関数の一部の変数に対する変化率を求める手法
- 物理・経済・機械学習など、多くの分野で応用される
- 勾配降下法などの最適化アルゴリズムにも使用される
📌 偏微分を理解することで、数学だけでなく、データ分析やAI分野にも応用できる知識が身につきます!

