確率論や統計学の基礎において、「ある事象が起こるか、起こらないか」を表現するのに便利な分布がベルヌーイ分布です。
例えば、
- コインを投げたときに表（1）が出る確率
- メールがスパム（1）かそうでない（0）か
- 機械が正常に作動するか（1）しないか（0）
このように、結果が**「成功」または「失敗」の二択** となる確率モデルを扱う際にベルヌーイ分布が使われます。本記事では、以下のポイントを解説します。
ベルヌーイ分布の基本概念と性質 実際のデータや応用例を用いた説明 Rによるシミュレーションと可視化
統計の基礎を学ぶ上で欠かせない分布なので、ぜひ理解を深めていきましょう！
1. ベルヌーイ分布の基礎知識
ベルヌーイ分布は、確率論や統計学における最も基本的な離散確率分布の一つです。本章では、ベルヌーイ分布の定義や確率質量関数、期待値と分散、二項分布との関係について詳しく解説します。
1-1 ベルヌーイ分布とは？
ベルヌーイ分布（Bernoulli distribution） とは、1回の試行の結果が「成功（1）」または「失敗（0）」のいずれかである確率分布 のことを指します。
このような試行を ベルヌーイ試行 と呼びます。
ベルヌーイ分布が使われる例
- コイン投げ（表が出る確率 pp ）
- 製品の検査（不良品でない確率 pp ）
- メールのスパム判定（スパムメールである確率 pp ）
このように、結果が「成功 or 失敗」「表 or 裏」のように2通りしかない場合に使われます。
1-2 確率質量関数（PMF）と性質
確率質量関数（PMF, Probability Mass Function） とは、離散確率変数が特定の値をとる確率を表す関数です。ベルヌーイ分布の確率質量関数は次のように定義されます。
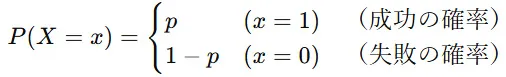
ここで、
- X はベルヌーイ分布に従う確率変数
- p は成功する確率（ 0≤p≤1 ）
1-3 ベルヌーイ分布の期待値と分散
確率変数 X がベルヌーイ分布 Bern(p)に従う場合、その期待値（平均） と 分散 は次のように求められます。
① 期待値（Expected Value）
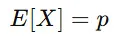
これは、「1が出る確率の平均は成功確率 pp に等しい」ということを意味します。
② 分散（Variance）
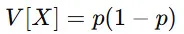
これは、「確率 p が0または1に近いほど、変動（ばらつき）が小さい」ことを示しています。
1-4 ベルヌーイ分布と二項分布の関係
ベルヌーイ分布は、二項分布（Binomial distribution） の特別な場合と考えることができます。
① 二項分布とは？
二項分布は、独立したベルヌーイ試行を n 回繰り返したときに成功する回数を表す確率分布 です。
確率変数 X が二項分布に従う場合、次のように表されます。
- ：試行回数（例：コインを10回投げる）
- p：成功確率（例：表が出る確率）
② ベルヌーイ分布との関係
ベルヌーイ分布は、二項分布の特別なケース（n= の場合） です。つまり、1回の試行の結果が「成功」か「失敗」かを扱う場合、ベルヌーイ分布と二項分布は同じになります。
2. ベルヌーイ分布の具体例と応用
ベルヌーイ分布は、単純な確率モデルですが、さまざまな分野で活用されています。本章では、ベルヌーイ分布の代表的な応用例を紹介します。
2-1 コイン投げの確率モデル
ベルヌーイ分布の最も基本的な例はコイン投げです。
- **表が出る確率を p **
- **裏が出る確率を 1− **
とすると、確率変数 XX は次のように定義されます。
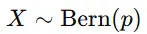
例えば、公正なコイン（p=0.5p = 0.5）の場合、
- P(X=1)=（表が出る確率）
- P(X=0)（裏が出る確率）
実際に、Rを使ってコイン投げのシミュレーションを行う方法は後の章で詳しく解説します。
2-2 スパムメールの分類
ベルヌーイ分布は、スパムメール分類 のような二値分類問題 でもよく使われます。
- X=（スパムメールである確率 p ）
- X=（スパムメールでない確率 1−p ）
この場合、スパムフィルターの判定結果がベルヌーイ分布に従う確率変数 で表されます。
機械学習では、こうしたデータを基にロジスティック回帰などの手法を適用し、スパムメールの判定精度を向上させます。
2-3 機械学習での活用（ロジスティック回帰との関連）
ロジスティック回帰（Logistic Regression） は、ベルヌーイ分布を基礎とする統計モデル です。
例えば、ある広告がクリックされる確率 を予測する場合、
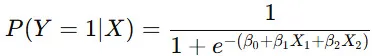
このように、シグモイド関数を用いて確率を求めるモデル となっています。
ロジスティック回帰は、ベルヌーイ分布を基礎としており、「確率的に分類を行う」ために利用されます。
3. Rを使ったベルヌーイ分布の実装
ここでは、Rを用いてベルヌーイ分布をシミュレーションし、確率質量関数（PMF）の可視化や平均・分散の確認 を行います。
3-1 Rでベルヌーイ分布をシミュレーション
Rでは、rbinom() 関数を用いてベルヌーイ分布に従う乱数を生成できます。
ベルヌーイ分布は二項分布（n=1） の特別なケースなので、以下のように実装できます。
① 1回の試行をシミュレーション
# 成功確率 p = 0.3 のベルヌーイ分布に従うデータを1回生成
set.seed(123) # 乱数の固定
rbinom(1, size = 1, prob = 0.3)
このコードを実行すると、0 または 1 のいずれかがランダムに出力されます。
（約30%の確率で「1」、70%の確率で「0」が出る）
② 100回の試行をシミュレーション
# p = 0.3 のベルヌーイ分布に従うデータを100回生成
data <- rbinom(100, size = 1, prob = 0.3)
# 生成したデータの確認
table(data)
このコードでは、100回の試行結果が data に格納されます。table(data) を実行すると、成功（1）と失敗（0）の出現回数が表示されます。
3-2 確率質量関数の可視化
次に、生成したデータをヒストグラムで可視化します。
# ヒストグラムのプロット
barplot(table(data) / length(data),
names.arg = c("0 (失敗)", "1 (成功)"),
col = c("blue", "red"),
main = "ベルヌーイ分布のシミュレーション結果",
xlab = "結果",
ylab = "確率")
- 青色の棒 →
0（失敗）の割合 - 赤色の棒 →
1（成功）の割合
このように、ベルヌーイ分布に従うデータが理論上の確率（p=0.3）に近い形で分布することを可視化 できます。
3-3 平均・分散の確認と検証
ベルヌーイ分布の期待値（平均） と 分散 は以下の式で求められます。
- 期待値（E[X]）: p
- 分散（V[X]）: p(1−p)
これをRで計算し、理論値と比較してみます。
① 実際の平均と分散を計算
# シミュレーションデータの平均（期待値）
mean(data)
# シミュレーションデータの分散
var(data)
② 理論値と比較
# 理論的な期待値と分散
p <- 0.3
expected_mean <- p
expected_var <- p * (1 - p)
print(paste("理論的な期待値:", expected_mean))
print(paste("理論的な分散:", expected_var))
4. Q＆A（よくある質問）
ここでは、ベルヌーイ分布についてよくある質問とその回答をまとめました。
Q1. ベルヌーイ分布と二項分布の違いは？
A. ベルヌーイ分布と二項分布は密接に関係していますが、試行回数に違いがあります。
| 分布 | 試行回数 | 例 |
|---|---|---|
| ベルヌーイ分布 | 1回（n=1） | 1回のコイン投げ |
| 二項分布 | n 回（n≥1） | 10回のコイン投げで表が出る回数 |
つまり、ベルヌーイ分布は「n=1 の二項分布」と考えることができます。
Q2. ベルヌーイ分布のパラメータ p はどのように決めるべき？
A. 実験データや過去の統計データをもとに決定します。
例として、
- コインの表が出る確率 → 物理的に 0.5 に設定可能
- スパムメールの確率 → 過去のデータから「スパムの割合」を推定
パラメータ p の推定には、最大尤度法（MLE） や ベイズ推定 が使われます。
Q3. ベルヌーイ分布はどんな場面で役に立つ？
A. ベルヌーイ分布は、Yes/No や 成功/失敗 のような分類問題 に適用できます。
応用例
- 医療データ：特定の病気にかかるかどうか（1=あり, 0=なし）
- マーケティング：顧客が広告をクリックするかどうか
- 品質管理：製品が不良品かどうか
Q4. シミュレーションで得られた平均と理論値が少し違うのはなぜ？
A. シミュレーション結果には標本誤差 があるため、試行回数が少ないと理論値と完全に一致しません。
実際のデータと理論値を近づけるには、試行回数を増やす（n を大きくする） 必要があります。
# 10000回の試行でベルヌーイ分布をシミュレーション
data_large <- rbinom(10000, size = 1, prob = 0.3)
# 平均と分散を確認
mean(data_large)
var(data_large)
試行回数を増やすと、理論値により近づくことを確認 できます。
5. まとめ
本記事では、ベルヌーイ分布について基礎から応用、Rでの実装まで詳しく解説しました。
ベルヌーイ分布のポイント
- 成功確率 p に基づく 2値（0または1） の確率分布
- コイン投げ、スパム分類、ロジスティック回帰など 幅広く活用される
- Rの
rbinom()を使ってシミュレーション可能 - 試行回数を増やすと理論値に近づく
ベルヌーイ分布が適している場面
- コイン投げやギャンブル
- バイナリ分類（スパムメールの判定など）
- マーケティングのA/Bテスト
本記事を参考に、ぜひ実際のデータでベルヌーイ分布を試してみてください！
確率論や統計学の基礎において、「ある事象が起こるか、起こらないか」を表現するのに便利な分布がベルヌーイ分布です。 例えば、 コインを投げたときに表（1）が出る確率 メールがスパム（1）かそうでない（0）か 機械が正常に作動するか（1）しないか（0） このように、結果が**「成功」または「失敗」の二択** となる確率モデルを扱う際にベルヌーイ分布が使われます。本記事では、以下のポイントを解説します。 ベルヌーイ分布の基本概念と性質 実際のデータや応用例を用いた説明' ...
統計分析を行う際、データの中に 外れ値（異常値） が含まれていることはよくあります。例えば、以下のようなケースが考えられます。 売上データにおいて、一部の異常に高い値がある 医療データで、極端に異常な検査結果が混ざっている センサー測定値にノイズが含まれ、誤ったデータが発生している このような異常値の影響を受けると、平均値や標準偏差などの統計量が歪み、本来のデータの傾向を適切に反映できなくなる 可能性があります。 この問題を解決するのが、ロバスト統計学（R ...
統計分析や機械学習において、説明変数（独立変数）同士が強い相関を持つこと は、回帰モデルの推定精度を低下させる可能性があります。 このような状況を 「多重共線性（Multicollinearity）」 と呼びます。 多重共線性が起こると何が問題か？ 回帰係数の推定値が不安定 になり、解釈が難しくなる 統計的な有意性（p値）が正しく評価できなくなる モデルの予測精度が低下 し、新しいデータに対して適用しにくくなる 例えば、以下のようなデータセットを考えます。 ...
統計分析において、「ある説明変数が目的変数に与える影響を評価したい」と考えることはよくあります。しかし、多くのデータには 複数の説明変数が同時に影響を及ぼしている ため、単純な単回帰分析では正しい評価ができないことがあります。 そこで活用されるのが 偏回帰分析（Partial Regression Analysis） です。 偏回帰分析の主な目的 特定の変数が目的変数に与える影響を、他の変数の影響を除外した上で評価する 多変量データの中で、各説明変数の相対的な寄与度を明確にする 重回帰分 ...
統計学において、「新しい情報を得たときに、既存の知識をどのように更新するか？」という問題は非常に重要です。その問題に答えるのがベイズ統計学 です。 ベイズ統計学（Bayesian Statistics） は、事前確率（prior probability）と新しいデータの尤度（likelihood）を組み合わせ、事後確率（posterior probability）を求めることで推論を行います。 例えば、以下のようなケースで活用されています。 医療診断：「ある検査で陽性が出た場合、本当に病 ...