統計分析を行う際、データの中に 外れ値（異常値） が含まれていることはよくあります。
例えば、以下のようなケースが考えられます。
売上データにおいて、一部の異常に高い値がある 医療データで、極端に異常な検査結果が混ざっている センサー測定値にノイズが含まれ、誤ったデータが発生している
このような異常値の影響を受けると、平均値や標準偏差などの統計量が歪み、本来のデータの傾向を適切に反映できなくなる 可能性があります。
この問題を解決するのが、ロバスト統計学（Robust Statistics） です。
ロバスト統計学とは？
- 外れ値の影響を最小限に抑える統計手法
- データの歪みがあっても、信頼性の高い推定値を提供できる方法
- 平均値ではなく中央値（Median） を使ったり、外れ値を抑制する手法を用いる
本記事では、
- ロバスト統計学の基本概念と代表的な手法
- Rを使ったロバスト統計学の実装
を解説していきます。
1. ロバスト統計学の基礎知識
ロバスト統計学は、外れ値や異常値の影響を受けにくい統計手法です。本章では、ロバスト統計の基本概念、外れ値が統計分析に与える影響、従来の統計手法との違い、ロバスト統計学が必要なケースについて詳しく解説します。
1-1 ロバスト統計学とは？
ロバスト統計学（Robust Statistics）とは、データに異常値や極端な値が含まれていても、分析結果が大きく変わらない統計手法のこと です。
例えば、平均値（Mean） は外れ値の影響を大きく受けますが、中央値（Median） は外れ値に強く、データの中心をより適切に表します。
ロバスト統計の特徴
外れ値の影響を最小限に抑える データの分布が正規分布でなくても安定した結果が得られる 偏りのあるデータでも信頼性のある推定が可能
1-2 外れ値（異常値）の影響とロバスト性の重要性
外れ値が統計分析に与える影響を可視化してみましょう。
① 外れ値の影響を受けやすい平均値
例えば、以下のデータを考えます。
#Rスクリプト
data <- c(10, 12, 14, 15, 16, 100) # 最後の値 "100" は外れ値
mean(data) # 平均値
median(data) # 中央値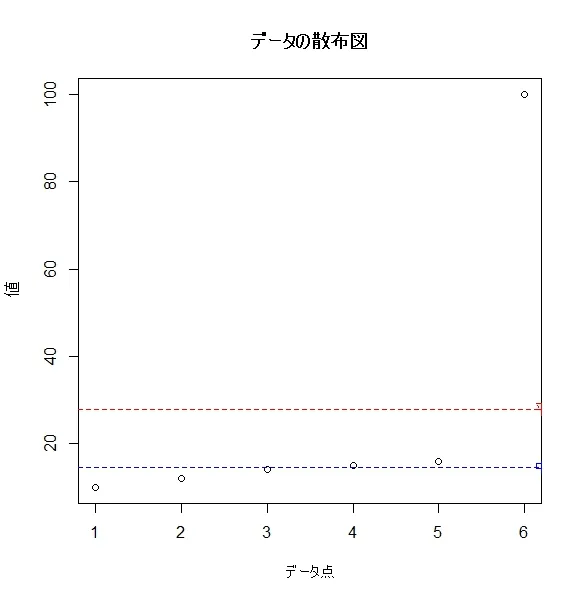
このデータでは、1つの外れ値（100）の影響で、平均値が大きく歪んでしまいます。
一方、中央値は外れ値の影響を受けにくいため、より適切な代表値を提供します。
平均値（Mean） = 27.83（外れ値の影響を大きく受ける） 中央値（Median） = 14.5（外れ値の影響を受けにくい）
② 平均値 vs. 中央値の比較（グラフ）
次のグラフは、外れ値がある場合の平均値と中央値の違いを示しています。
# 必要なパッケージを読み込む
install.packages("ggplot2")
library(ggplot2)
# データフレームを作成
data <- data.frame(
値 = c(10, 12, 14, 15, 16, 100)
)
# 平均値と中央値の計算
mean_value <- mean(data$値)
median_value <- median(data$値)
# データのプロット
ggplot(data, aes(x = "", y = 値)) +
geom_boxplot(fill = "lightblue") +
geom_hline(yintercept = mean_value, color = "red", linetype = "dashed", size = 1.2) +
geom_hline(yintercept = median_value, color = "blue", linetype = "dashed", size = 1.2) +
labs(title = "外れ値の影響：平均値 vs. 中央値",
y = "データの値") +
annotate("text", x = 1.2, y = mean_value + 5, label = paste("平均値:", round(mean_value, 2)), color = "red") +
annotate("text", x = 1.2, y = median_value - 5, label = paste("中央値:", round(median_value, 2)), color = "blue")
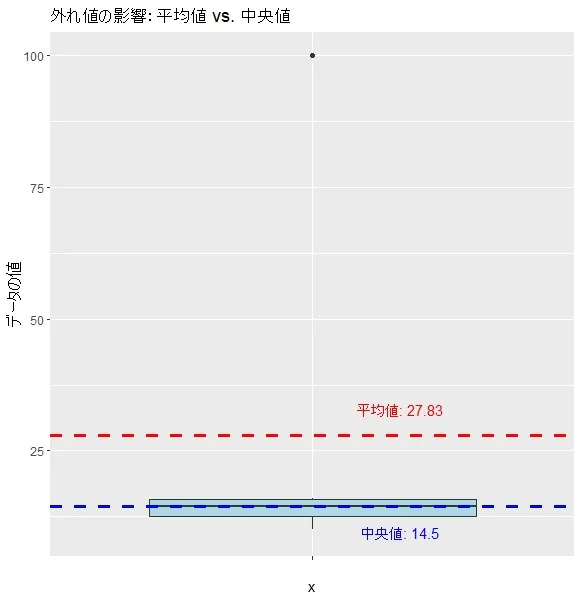
赤線（平均値）は外れ値の影響で大きくズレていますが、青線（中央値）はほとんど影響を受けていません。
1-3 ロバスト統計と従来の統計手法の違い
ロバスト統計は、従来の統計手法よりも外れ値に対する耐性があります。
| 指標 | 従来の統計手法 | ロバスト統計手法 |
|---|---|---|
| 代表値 | 平均値（Mean） | 中央値（Median）、トリム平均 |
| 散布度 | 標準偏差（SD） | 中央絶対偏差（MAD）、四分位範囲（IQR） |
| 回帰分析 | 最小二乗法（OLS） | ロバスト回帰（M推定、Theil-Sen推定） |
| 相関分析 | ピアソン相関係数 | スピアマン相関係数 |
ロバスト統計は、外れ値がある場合でも、より頑健な（信頼できる）分析結果を提供できます。
1-4 ロバスト統計学が必要なケース
ロバスト統計が必要なケースとして、次のような状況が考えられます。
① 実験データやセンサーデータにノイズが含まれている
- 科学実験のデータには測定誤差やセンサーの異常値が含まれることが多い
- ロバスト統計を使うことで、異常値の影響を抑えた分析が可能
② 金融データやマーケティングデータの分析
- 売上データや株価データには突発的な異常値（急激な変動）が存在する
- 平均値ではなく、中央値やロバスト回帰を用いることで、より正確な分析ができる
③ 医療データの統計分析
- 血糖値や心拍数などの医療データでは、一部の異常値が含まれる可能性が高い
- 標準偏差よりも、IQR（四分位範囲）やMAD（中央値絶対偏差）を使うことで、信頼性の高い統計解析が可能
2. ロバスト統計の代表的な手法と応用
ロバスト統計学には、外れ値に強いさまざまな手法があります。本章では、代表値のロバスト推定、分散と散布度のロバスト推定、外れ値に強い回帰分析 について解説し、Rでの実装例を紹介します。
2-1 外れ値に強い代表値（中央値・トリム平均・Winsorized 平均）
従来の代表値（平均値）は外れ値の影響を受けやすいため、ロバストな手法が必要です。
① 中央値（Median）
中央値は、データを昇順に並べたときの中央の値です。
# 中央値の計算
data <- c(10, 12, 14, 15, 16, 100) # 外れ値100を含む
median(data) # 出力: 14.5
外れ値の影響を受けにくいので、分布が歪んでいるデータでも適切な代表値を示す。
② トリム平均（Trimmed Mean）
トリム平均は、データの上下何％かを削除し、その後の平均を計算する方法 です。
# トリム平均（10%カット）
mean(data, trim = 0.1) # 上下10%をカット 外れ値を除外して平均を計算するため、ロバスト性が向上する。
③ Winsorized 平均
Winsorized 平均は、外れ値を単純に除去するのではなく、最も大きな値と最も小さな値を「しきい値」に変換する方法 です。
# Winsorized 平均の計算
install.packages("DescTools")
library(DescTools)
WinsorMean(data, probs = 0.1) # 上下10%のデータをWinsor化 極端な値を調整しながら、分布の情報を保つ。
2-2 分散と散布度のロバスト推定（MAD・IQR）
従来の標準偏差（SD） は外れ値の影響を受けやすいため、ロバストな分散の指標が必要です。
① 中央絶対偏差（MAD：Median Absolute Deviation）
MAD は、中央値を基準とした偏差の中央値を求める方法です。
# MADの計算
mad(data) 標準偏差よりも外れ値の影響を受けにくい。
② 四分位範囲（IQR：Interquartile Range）
IQR は、データの 第1四分位数（Q1）と第3四分位数（Q3）の差 を用いた散布度の指標です。
# IQRの計算
IQR(data) 外れ値を考慮せず、データの中央50%の範囲を測定する。
MAD vs. 標準偏差の比較グラフ
# データの分布を可視化
library(ggplot2)
df <- data.frame(値 = data)
ggplot(df, aes(x = "", y = 値)) +
geom_boxplot(fill = "lightblue") +
geom_hline(yintercept = mean(data), color = "red", linetype = "dashed", size = 1) +
geom_hline(yintercept = median(data), color = "blue", linetype = "dashed", size = 1) +
labs(title = "標準偏差 vs. MAD", y = "データの値") +
annotate("text", x = 1.2, y = mean(data) + 5, label = paste("標準偏差:", round(sd(data), 2)), color = "red") +
annotate("text", x = 1.2, y = median(data) - 5, label = paste("MAD:", round(mad(data), 2)), color = "blue") 標準偏差（赤線）は外れ値の影響で大きく変動するが、MAD（青線）は安定している。
2-3 外れ値に強い回帰分析（ロバスト回帰・M推定）
従来の回帰分析（最小二乗法 OLS）は外れ値の影響を受けやすいため、ロバスト回帰を使用することで、より頑健な推定が可能です。
① Theil-Sen 推定
Theil-Sen 推定は、すべての点のペアの傾きを計算し、その中央値を回帰係数とする方法 です。
install.packages("mblm")
library(mblm)
# Theil-Sen 推定の実行
data_x <- c(1, 2, 3, 4, 5, 6, 7, 8, 9, 10)
data_y <- c(2, 3, 5, 7, 11, 13, 100, 19, 23, 29) # 100が外れ値
model <- mblm(data_y ~ data_x)
summary(model) 外れ値の影響を抑えながら、頑健な回帰モデルを構築できる。
② MM推定 MM推定は、M推定のロバスト性を向上させた手法であり、外れ値の影響を最小限に抑えつつ、高精度な回帰分析を行うことが可能 です。
install.packages("robustbase")
library(robustbase)
# MM推定によるロバスト回帰
robust_model <- lmrob(data_y ~ data_x)
summary(robust_model)
MM推定は、通常のOLS回帰と比較して外れ値の影響を受けにくく、より信頼性の高い回帰分析が可能。
OLS vs. ロバスト回帰の比較グラフ
library(ggplot2)
df <- data.frame(x = data_x, y = data_y)
ggplot(df, aes(x = x, y = y)) +
geom_point(color = "blue") +
geom_smooth(method = "lm", se = FALSE, color = "red", linetype = "dashed") +
geom_smooth(method = "mblm", se = FALSE, color = "green", linetype = "solid") +
labs(title = "OLS回帰 vs. Theil-Sen回帰",
x = "X（説明変数）",
y = "Y（目的変数）") +
theme_minimal()
赤線（OLS回帰）は外れ値の影響を受けて傾きが大きく変化するが、緑線（Theil-Sen回帰）は外れ値の影響を受けにくい。
3. Rを使ったロバスト統計の実装
ここでは、Rを用いてロバスト統計学の具体的な手法を実装し、外れ値の検出・ロバスト統計量の計算・ロバスト回帰の適用 を行います。
3-1 外れ値の検出と可視化（箱ひげ図・Zスコア）
ロバスト統計を適用する前に、データの中に外れ値が含まれているかどうかを確認することが重要 です。
① 箱ひげ図（Boxplot）を用いた外れ値の可視化
# サンプルデータ
data <- c(10, 12, 14, 15, 16, 100) # 外れ値100を含む
# 箱ひげ図の作成
boxplot(data, main = "箱ひげ図による外れ値の検出",
col = "lightblue", ylab = "値")
箱ひげ図では、四分位範囲（IQR）の範囲を超えた点が外れ値としてマークされます。
② Zスコアを用いた外れ値の検出 Zスコアを用いることで、データの標準偏差からの偏差を基準に外れ値を判断できます。
# Zスコアの計算
z_scores <- scale(data)
# Zスコアが ±2 を超えるデータを外れ値と判定
outliers <- data[abs(z_scores) > 2]
print(outliers)
Zスコアが ±2 を超えるデータ（ここでは 100）が外れ値として検出されます。
3-2 ロバスト統計量（中央値・MAD）の計算
① 中央値（Median）とトリム平均（Trimmed Mean）
# 中央値の計算
median(data)
# トリム平均（10%カット）
mean(data, trim = 0.1)
トリム平均はデータの上下10%を除外した平均値を計算するため、外れ値の影響を軽減できます。
② 中央絶対偏差（MAD）と四分位範囲（IQR）
# MADの計算
mad(data)
# IQRの計算
IQR(data)
標準偏差ではなくMADを使用することで、よりロバストな分散の評価が可能になります。
3-3 ロバスト回帰の実装（MM推定・Theil-Sen推定）
従来の回帰分析（OLS）とロバスト回帰を比較し、外れ値の影響を確認します。
① OLS回帰（通常の回帰分析）
# サンプルデータ
data_x <- c(1, 2, 3, 4, 5, 6, 7, 8, 9, 10)
data_y <- c(2, 3, 5, 7, 11, 13, 100, 19, 23, 29) # 外れ値100を含む
# 通常の回帰分析（OLS）
ols_model <- lm(data_y ~ data_x)
summary(ols_model)
OLS回帰は外れ値100の影響を強く受け、傾きが大きく変化します。
② Theil-Sen推定
install.packages("mblm")
library(mblm)
# Theil-Sen 推定の実行
robust_model <- mblm(data_y ~ data_x)
summary(robust_model)
Theil-Sen推定では、外れ値の影響を抑えた頑健な回帰モデルが構築されます。
③ MM推定（よりロバストな回帰手法）
install.packages("robustbase")
library(robustbase)
# MM推定によるロバスト回帰
mm_model <- lmrob(data_y ~ data_x)
summary(mm_model)
MM推定は、外れ値の影響を最小限に抑えながら、高精度な回帰分析が可能です。
OLS回帰 vs. ロバスト回帰の比較グラフ
library(ggplot2)
df <- data.frame(x = data_x, y = data_y)
ggplot(df, aes(x = x, y = y)) +
geom_point(color = "blue") +
geom_smooth(method = "lm", se = FALSE, color = "red", linetype = "dashed") + # OLS回帰
geom_smooth(method = "mblm", se = FALSE, color = "green", linetype = "solid") + # Theil-Sen推定
labs(title = "OLS回帰 vs. Theil-Sen回帰",
x = "X（説明変数）",
y = "Y（目的変数）") +
theme_minimal()
赤線（OLS回帰）は外れ値の影響を受けて傾きが大きく変化するが、緑線（Theil-Sen回帰）は外れ値の影響を受けにくい。
4. Q＆A（よくある質問）
ここでは、ロバスト統計学に関するよくある質問とその回答をまとめました。
Q1. ロバスト統計学は常に使うべきなのか？
A. ロバスト統計は外れ値に強い分析手法ですが、必ずしも常に使うべきではありません。
ロバスト統計が適しているケース
- 外れ値が多く含まれるデータ（例：センサーデータ、医療データ）
- 分布が正規分布から大きく逸脱しているデータ
- 回帰分析で外れ値の影響を最小限にしたい場合
通常の統計手法で十分なケース
- 外れ値がほとんど存在しない場合
- データがきれいな正規分布に従っている場合
- 小規模データで、ロバスト手法が逆に精度を下げる可能性がある場合
結論：データの性質に応じてロバスト統計と従来の統計手法を使い分けることが重要。
Q2. ロバスト回帰と通常のOLS回帰はどう違うの？
A. OLS回帰（最小二乗法）とロバスト回帰の主な違いは、外れ値の影響をどれだけ受けるかです。
| 手法 | 外れ値の影響 | 計算方法 | 適用例 |
|---|---|---|---|
| OLS回帰 | 影響を大きく受ける | 残差の二乗和を最小化 | 正規分布のデータ分析 |
| Theil-Sen推定 | 影響を受けにくい | 全ペアの傾きの中央値 | 統計分析、環境データ |
| MM推定 | 影響をほぼ受けない | M推定＋効率性の最適化 | 医療データ、マーケティング |
OLS回帰は外れ値に敏感だが、ロバスト回帰は外れ値の影響を抑えることができる。
Q3. ロバスト統計とベイズ統計の違いは？
A. ロバスト統計とベイズ統計は、それぞれ異なる目的を持っています。
| 特徴 | ロバスト統計 | ベイズ統計 |
|---|---|---|
| 主な目的 | 外れ値の影響を抑える | 事前確率と新しいデータの統合 |
| 適用範囲 | データの頑健性を確保 | 確率分布を用いた推定 |
| 手法例 | 中央値、MAD、ロバスト回帰 | ベイズ推定、MCMC |
外れ値対策ならロバスト統計、確率推定ならベイズ統計を使うのが適切。
Q4. ロバスト統計は機械学習にも応用できる？
A. はい、ロバスト統計の考え方は機械学習にも応用可能です。
機械学習への応用例
-
ロバスト回帰を用いた回帰モデルの改良
- Theil-Sen推定やHuber回帰を使用すると、外れ値の影響を受けにくい回帰モデルが作成できる。
-
異常検知（Anomaly Detection）
- IQR（四分位範囲）やMADを用いて、異常値を検出し、データクリーニングに活用。
-
分類問題への適用
- 標準的なロジスティック回帰ではなく、ロバストロジスティック回帰を使うことで、外れ値の影響を最小限にできる。
ロバスト統計は、データの前処理や異常値検出において、機械学習の精度を向上させるのに有効。
5. まとめ
本記事では、ロバスト統計学について基礎から応用、Rでの実装まで詳しく解説しました。
ロバスト統計のポイント
- 外れ値の影響を受けにくい統計手法
- 中央値・MAD・ロバスト回帰を活用すると頑健な分析が可能
- データの特性に応じて、従来の統計手法と使い分けることが重要
ロバスト統計が適している場面
- 金融データ：異常な値を含む株価の分析
- 医療データ：血糖値や心拍数の外れ値の影響を抑える
- マーケティング：売上や広告費データの頑健な解析
- 機械学習：外れ値の影響を受けにくいモデルの構築
ロバスト統計学は、実データの分析において非常に重要な手法です。本記事を参考に、Rを使って実際にロバスト統計を試してみてください！
統計分析や機械学習において、説明変数（独立変数）同士が強い相関を持つこと は、回帰モデルの推定精度を低下させる可能性があります。 このような状況を 「多重共線性（Multicollinearity）」 と呼びます。 多重共線性が起こると何が問題か？ 回帰係数の推定値が不安定 になり、解釈が難しくなる 統計的な有意性（p値）が正しく評価できなくなる モデルの予測精度が低下 し、新しいデータに対して適用しにくくなる 例えば、以下のようなデータセットを考えます。 ...
統計分析において、「ある説明変数が目的変数に与える影響を評価したい」と考えることはよくあります。しかし、多くのデータには 複数の説明変数が同時に影響を及ぼしている ため、単純な単回帰分析では正しい評価ができないことがあります。 そこで活用されるのが 偏回帰分析（Partial Regression Analysis） です。 偏回帰分析の主な目的 特定の変数が目的変数に与える影響を、他の変数の影響を除外した上で評価する 多変量データの中で、各説明変数の相対的な寄与度を明確にする 重回帰分 ...
統計学において、「新しい情報を得たときに、既存の知識をどのように更新するか？」という問題は非常に重要です。その問題に答えるのがベイズ統計学 です。 ベイズ統計学（Bayesian Statistics） は、事前確率（prior probability）と新しいデータの尤度（likelihood）を組み合わせ、事後確率（posterior probability）を求めることで推論を行います。 例えば、以下のようなケースで活用されています。 医療診断：「ある検査で陽性が出た場合、本当に病 ...