統計学は、数字を通じて、世の中の不確実性に秩序をもたらす魅力的な分野です。今日は、統計学における二つの基本的な概念「検出力」と「サンプルサイズ」について、初心者の方にもわかりやすく説明します。
1. 検出力の基本
「検出力」とは、統計的検定が本当に効果がある場合に、その効果を見つけることができる確率です。これは統計的なテストの「感度」とも言えます。
具体例:新薬の効果を検証する
想像してみてください。ある新薬Aが特定の病気に対して効果があるかどうかを調べる臨床試験を行うとします。ここでの「検出力」は、新薬Aが効果がある場合に、その効果を実際に検出できるテストの能力を指します。
2. サンプルサイズの重要性
次に、「サンプルサイズ」についてです。これは実験や調査でデータを集める個体の総数を意味します。新薬Aの試験における参加者の数が、まさにこれに当たります。
検出力とサンプルサイズの関係
検出力とサンプルサイズは直接的な関係があります。一般に、サンプルサイズが大きいほど、より小さい効果を検出する能力が高まります。要するに、検出力を高めるにはサンプルサイズを増やす必要があります。
3. 必要なサンプルサイズの計算
ただし、単にサンプルサイズを増やすのではなく、効率的な研究設計のためには適切なサンプルサイズを計算することが肝心です。これには、効果の大きさ(効果量)、許容する誤差の範囲(αレベル)、目指す検出力(例えば80%)が必要になります。
新薬Aの事例における計算
新薬Aの例に戻ると、仮に10%の改善効果を期待する場合、この10%の差を検出するためにどのくらいのサンプルサイズが必要かを計算します。サンプルサイズが不十分だと、たとえ本当に差があったとしてもそれを見逃してしまう可能性があります。過剰にサンプルサイズを増やせば、無駄なコストと時間を要します。
統計ソフトウェアを用いると、これらの要因を入力するだけで、必要なサンプルサイズを簡単に計算できます。
統計学の提供するツール
統計学は予測不可能な現象に対して合理的な推測を行うためのツールを提供します。検出力とサンプルサイズは統計的な意思決定において不可欠な要素であり、適切な計画をもって実験や調査に臨むことで、結果の信頼性を高めることができます。
Rで検出力を計算してみよう
power.t.test は R 言語で利用できる関数で、検出力(power)、サンプルサイズ(n)、効果量(effect size)、および有意水準(significance level)の関係を計算するのに使われます。特に t 検定を行う際に、事前に必要なサンプルサイズを計算したり、特定のサンプルサイズでの検出力を求めたりするときに有用です。
以下に power.t.test の基本的な使い方を示します。
1. サンプルサイズの計算
効果量と検出力、有意水準を指定して、必要なサンプルサイズを計算する。
power.t.test(n= サンプルサイズ、delta = 効果量, power = 検出力, sig.level = 有意水準, type = "two.sample", alternative = "two.sided")
サンプルサイズだけ「NULL」として、仮に効果量を0.8、検出力を0.8、有意水準を0.05として計算すると以下のようになります。
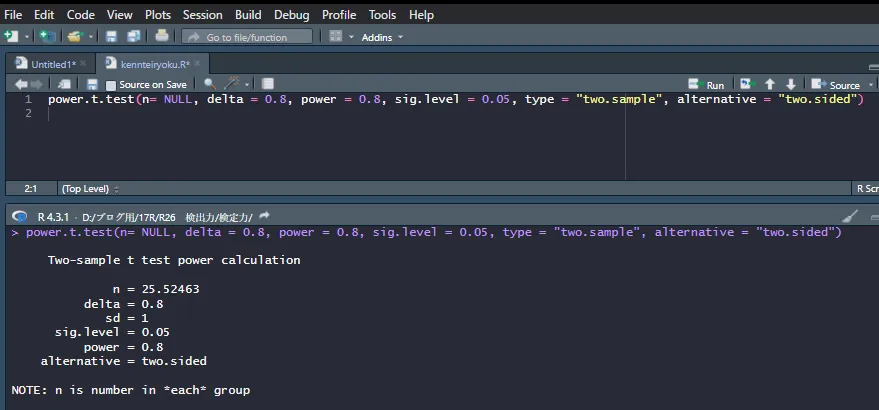
n=25.25463と出ました。必要なサンプルサイズが各群について出力されています。
効果量を0.8くらいの差を、0.8の検出力で有意水準を0.05とした、検定結果を得るのに必要なサンプルサイズは各群25個程度のサンプル数が必要ということがこれで分かります。
2. 検出力の計算
同様にして検出力を掲載したい場合は、効果量とサンプルサイズ、有意水準を指定して、検出力を計算しましょう。
効果量を0.8、サンプルサイズ5個、有意水準0.05として検出力を計算してみましょう。

検出力は0.1997421と計算されました。
検出力の目安は?
検出力(power)は、統計的検定が実際に効果や差を検出する能力を表しており、通常は0.8(80%)以上を目安として設定されます。検出力が0.8であるということは、実際に効果が存在する場合に80%の確率でその効果を検出するテストの能力があることを意味します。これは、統計的検定で第II種の誤り(β)を犯すリスクが20%であることと対応しています。
検出力の選択は研究の文脈や目的によって異なる場合があります。以下は一般的な目安です:
- 0.8(80%): 標準的な目安で、多くの社会科学や行動科学、医学研究で使用されています。
- 0.9(90%): より高い検出力が望まれる場合、特に結果が重要な意思決定に影響を与える研究ではこの値が選ばれることがあります。
- 0.7(70%)以下: 限られた資源や実現不可能なサンプルサイズの場合、低い検出力が選ばれることもありますが、この場合、見逃すリスクが高まります。
実際には、研究の設計段階で、効果の大きさ、サンプルサイズ、検出力、有意水準(α)をバランスさせながら最適な計画を立てる必要があります。検出力が高ければ高いほど良いというわけではありません。検出力を上げるためには通常、より多くのサンプルサイズが必要となり、それにはより多くの費用と時間がかかります。また、非常に小さな効果も検出するように設計された研究は、実用的な意味合いのある効果を見逃す可能性が低くなりますが、一方で、非常に小さな効果が統計的に有意であると報告するリスクが高まります。
結論として、検出力は研究ごとに異なる目的や条件に応じて慎重に選択されるべきです。研究者は、必要な検出力を確実に得るために、どれだけのリソースを投入する準備があるかを考慮する必要があります。
3. 効果量の計算
やり方は同様にして、サンプルサイズと検出力、有意水準を指定して、検出できる最小の効果量を計算しましょう。
サンプルサイズを10、検出力を0.8、有意水準0.05を指定して、検出できる最小の効果量を計算してみると次のようになります。
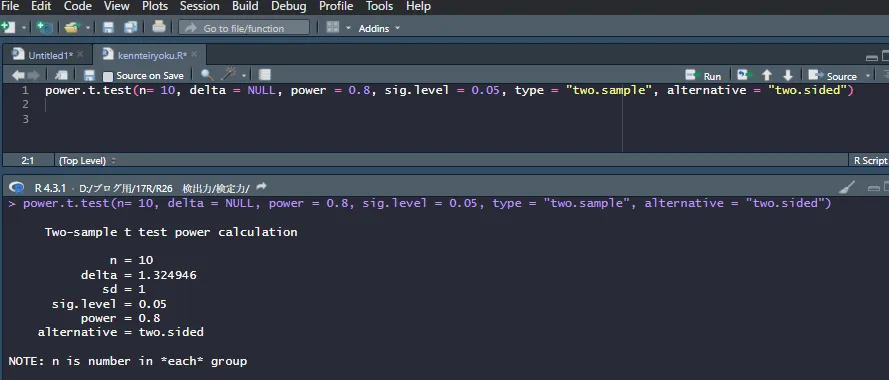
検出できる最小の効果量は1.324946と出ました。
主要な引数
n:サンプルサイズdelta:効果量(平均の差や効果の大きさ)sd:母集団の標準偏差(省略可能で、デフォルトは 1)sig.level:有意水準(デフォルトは 0.05)power:検出力(例えば 0.8 または 80%)type:検定のタイプ("one.sample"、"two.sample"、または "paired")alternative:代替仮説が「片側」か「両側」か("one.sided" または "two.sided")
power.t.test 関数を使う際には、一つの引数としてサンプルサイズ(n)、効果量(delta)、検出力(power)、または有意水準(sig.level)のうち3つを指定し、残りの1つを計算する形になります。指定されなかった引数は関数によって計算され、どのような研究デザインでどの程度の効果が検出可能かの目安を得ることができます。

