統計学において、「新しい情報を得たときに、既存の知識をどのように更新するか?」という問題は非常に重要です。その問題に答えるのがベイズ統計学 です。
ベイズ統計学(Bayesian Statistics) は、事前確率(prior probability)と新しいデータの尤度(likelihood)を組み合わせ、事後確率(posterior probability)を求めることで推論を行います。
例えば、以下のようなケースで活用されています。
✅ 医療診断:「ある検査で陽性が出た場合、本当に病気である確率は?」
✅ スパムフィルター:「特定の単語が含まれるメールがスパムである確率は?」
✅ マーケティング分析:「広告をクリックしたユーザーが購入する確率は?」
本記事では、
- ベイズの定理の基本概念
- 実際のデータを用いた応用例
- Rを用いた実装方法
を解説していきます。確率論を理解する上で非常に重要な内容ですので、ぜひ最後まで読んでみてください!
1. ベイズ統計学の基礎知識
ベイズ統計学は、確率を「信念の更新」として捉え、新しい情報が得られるたびに確率を更新していく統計手法 です。本章では、ベイズ統計学の基本概念、ベイズの定理の数式、事前確率・事後確率の考え方、頻度主義との違いについて詳しく解説します。
1-1 ベイズ統計学とは?
ベイズ統計学(Bayesian Statistics) は、「新しいデータを得たときに、どのように確率を修正するか?」 という問題を扱います。
例えば、ある医療検査で陽性(positive)と判定されたとき、
「本当に病気である確率はどのくらいか?」
と考えた場合、検査の精度や病気の発生率(事前情報)を考慮 しなければなりません。
このような「新しい情報を加味した確率の更新」を数学的に扱うのがベイズ統計学 です。
1-2 ベイズの定理の数式と直感的な理解
ベイズ統計の中心となるのは、ベイズの定理(Bayes’ theorem) です。
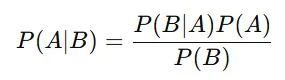
この式を分解すると、
- P(A∣B):Bというデータが得られたときのAの確率(事後確率)
- P(B∣A):Aが起こったときにBが起こる確率(尤度)
- P(A):Aが起こる事前の確率(事前確率)
- P(B):Bが起こる全体の確率(周辺確率)
直感的な理解
ベイズの定理は、次のように考えると分かりやすくなります。
✅ 新しい情報(B)を得たとき、もともとの知識(Aの確率)をどのように修正すればよいか?
✅ 「BのもとでAが発生する確率(事後確率)」は、「Aが発生する確率(事前確率)」と「BのもとでAが発生する確率(尤度)」を掛け合わせたもので決まる。
1-3 事前確率・尤度・事後確率とは?
ベイズの定理の各要素について詳しく説明します。
① 事前確率(Prior Probability)
P(A)
- 事前情報や経験から得られる確率
- 例:「ある病気の発生確率は人口の1%」
② 尤度(Likelihood)
P(B∣A)
- Aが起こったときにBが起こる確率
- 例:「病気の人が検査を受けたときに陽性と判定される確率(検査の精度)」
③ 事後確率(Posterior Probability)
P(A∣B)
- 新しいデータ(B)が得られた後の確率
- 例:「検査で陽性が出たとき、本当に病気である確率」
ベイズの定理では、事前確率を更新し、事後確率を計算することで、確率のより正確な推定を可能にします。
1-4 ベイズ統計と頻度主義統計の違い
統計学には、ベイズ統計 と 頻度主義統計(Frequentist Statistics) という2つの異なる考え方があります。
| 比較項目 | ベイズ統計学 | 頻度主義統計 |
|---|---|---|
| 確率の解釈 | 主観的(信念の更新) | 客観的(長期的頻度) |
| 必要な情報 | 事前確率を考慮する | データのみで推定する |
| 仮説検定 | 事後確率を求める | p値を用いて帰無仮説を棄却するか決定 |
| 例 | 医療診断、マーケティング分析 | 実験データの統計解析 |
例:病気の診断
- 頻度主義統計:「この検査は99%の精度で病気を検出できる」
- ベイズ統計:「ある人が陽性と診断されたとき、本当に病気である確率は?」(病気の発生率を考慮)
このように、ベイズ統計は「不確実性の中での推論」に適しており、近年では機械学習やデータ分析の分野で広く利用されています。
2. ベイズ統計学の具体例と応用
ベイズ統計学は、さまざまな分野で活用されています。本章では、医療診断、スパムフィルター、データ分析の改善 という3つの具体例を通じて、ベイズの定理がどのように適用されるのかを詳しく解説します。
2-1 医療診断におけるベイズ推論
例題:「がん検査の結果が陽性だったとき、本当にがんである確率は?」
あるがん検査は、以下のような精度を持っています。
- がんの発生率(事前確率): 1%(つまり、100人に1人ががんにかかる)
- 陽性率(尤度): 実際にがんのある人が陽性と診断される確率は90%(感度)
- 偽陽性率: 健康な人が誤って陽性と診断される確率は5%
これらの情報をベイズの定理に当てはめると、
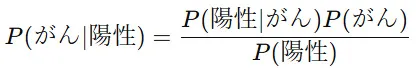
ここで、全体の陽性率は
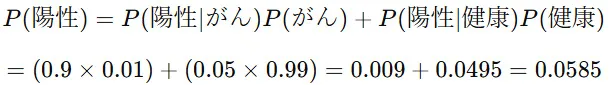
したがって、がんである確率(事後確率)は
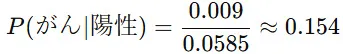
つまり、検査で陽性と診断されても、実際にがんである確率は約15.4%にすぎない ことが分かります。
この結果は、頻度主義統計(単純な陽性的中率)では考慮されない「事前確率」をベイズ推論が取り入れていることを示しています。
2-2 スパムフィルターとベイズの定理
Gmail などのメールサービスでは、ベイズ推論を活用してスパムメールを識別しています。
例:「ある単語(例:'無料')がメールに含まれていたとき、そのメールがスパムである確率は?」
仮に以下のデータがあったとします。
- スパムメールの割合(事前確率): 20%(全メールのうち20%がスパム)
- スパムメールに「無料」が含まれる確率(尤度): 70%
- 通常のメールに「無料」が含まれる確率(偽陽性率): 10%
この情報をベイズの定理に適用すると、スパムである確率(事後確率)は
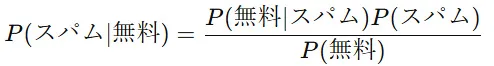
全体の「無料」の出現率は
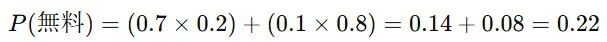
したがって、
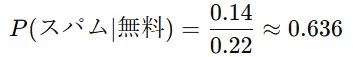
つまり、「無料」という単語が含まれていた場合、そのメールがスパムである確率は約63.6% となります。
このように、ベイズ推論を使うことで、単語の出現頻度と過去のデータからスパム判定の精度を向上させる ことができます。
2-3 ベイズ推定によるデータ分析の改善
ベイズ推定(Bayesian Estimation)は、パラメータ推定においても強力な手法 です。
① 頻度主義 vs. ベイズ推定
頻度主義の手法(例えば最尤推定)は、「データが与えられたときに最も可能性の高いパラメータ」を求めますが、ベイズ推定では、パラメータ自体を確率分布として扱い、事前情報を加味して推定を行います。
② ベイズ更新の例
例えば、ある新商品の売上予測を行う場合、過去の売上データ(事前確率)に基づき、新しいデータが入るたびに確率分布を更新することで、より正確な予測を行うことができます。
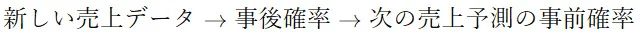
この方法は、マーケティングや経済予測、医療診断など、さまざまな分野で応用されています。
3. Rを使ったベイズ統計学の実装
ここでは、Rを用いてベイズ推論をシミュレーションし、ベイズの定理の計算・ベイズ推定・MCMC(マルコフ連鎖モンテカルロ法)による事後分布の推定 などを実装します。
3-1 Rでベイズの定理をシミュレーション
① がん検査の陽性的中率を求める
先ほどの 「がん検査の結果が陽性だったとき、本当にがんである確率」 を R で計算します。
# 事前確率(がんの発生率)
P_A <- 0.01
# 尤度(がん患者が陽性と診断される確率)
P_B_given_A <- 0.9
# 偽陽性率(健康な人が誤って陽性と診断される確率)
P_B_given_not_A <- 0.05
# 周辺確率(全体の陽性率)
P_B <- (P_B_given_A * P_A) + (P_B_given_not_A * (1 - P_A))
# 事後確率(陽性のときにがんである確率)
P_A_given_B <- (P_B_given_A * P_A) / P_B
# 結果の表示
print(paste("検査が陽性のとき、実際にがんである確率:", round(P_A_given_B, 3)))
このコードを実行すると、約15.4% という値が出力されるはずです。
3-2 ベイズ推定を用いたパラメータ推定
ベイズ推定では、パラメータを確率分布として推定 します。
ここでは、コイン投げの確率 pp をベイズ推定 する例を示します。
① ベータ分布を事前分布として使用
事前確率として、ベータ分布(Beta Distribution) を用います。
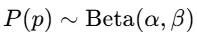
ここで、
- α(成功回数の事前情報)
- β(失敗回数の事前情報)
例えば、これまでの経験から「コインが表になる確率は約 50% だろう」と考えると、事前分布として Beta(2,2)\text{Beta}(2,2) を選択できます。
# ベータ分布をプロット
curve(dbeta(x, 2, 2), from = 0, to = 1, col = "blue", lwd = 2,
main = "事前分布:Beta(2,2)", xlab = "p(コインの表が出る確率)", ylab = "密度")
② データを観測し、事後分布を更新
10回のコイン投げで 7回 表 が出た場合、ベイズ更新を行います。
事後分布のパラメータは以下のように更新されます。

# 事前分布のパラメータ
alpha_prior <- 2
beta_prior <- 2
# 観測データ(7回成功, 3回失敗)
successes <- 7
failures <- 3
# 事後分布のパラメータ更新
alpha_posterior <- alpha_prior + successes
beta_posterior <- beta_prior + failures
# 事後分布のプロット
curve(dbeta(x, alpha_posterior, beta_posterior), from = 0, to = 1, col = "red", lwd = 2,
main = "事後分布:Beta(9,5)", xlab = "p(コインの表が出る確率)", ylab = "密度")
この結果、観測データを反映した事後分布が得られます。
3-3 MCMC(マルコフ連鎖モンテカルロ法)の基礎
ベイズ推定では、複雑な事後分布を求める際に MCMC(Markov Chain Monte Carlo) を用います。
ここでは、Rの rjags パッケージを使って MCMC を実行し、事後分布を推定します。
① 必要なパッケージのインストール
install.packages("rjags")
library(rjags)
② JAGS(Just Another Gibbs Sampler)を使ったベイズ推定
# JAGSモデルの記述
model_string <- "
model {
for (i in 1:N) {
y[i] ~ dbern(p)
}
p ~ dbeta(2, 2) # 事前分布
}
"
# データの準備
data_list <- list(y = c(1, 1, 1, 1, 1, 1, 1, 0, 0, 0), N = 10)
# JAGSモデルの設定
model <- jags.model(textConnection(model_string), data = data_list, n.chains = 3)
# サンプリングの実行
update(model, 1000) # バーンイン
samples <- coda.samples(model, variable.names = c("p"), n.iter = 5000)
# 結果のプロット
plot(samples)
このコードを実行すると、サンプリングされた事後分布がプロットされ、コインの表が出る確率 p の推定値が得られます。
4. Q&A(よくある質問)
ここでは、ベイズ統計学に関するよくある質問とその回答をまとめました。
Q1. ベイズ統計と頻度主義統計はどちらが優れているの?
A. 一概にどちらが優れているとは言えません。用途によって適した手法を選択することが重要です。
| 比較項目 | ベイズ統計 | 頻度主義統計 |
|---|---|---|
| 確率の解釈 | 主観的(信念の更新) | 客観的(長期的頻度) |
| 事前情報の利用 | 可能(事前確率を考慮) | 不可(データのみで推定) |
| 結果の表現 | 事後確率分布 | 点推定やp値 |
| 適用例 | 医療診断、機械学習、マーケティング | 仮説検定、実験データの分析 |
✅ データが少ない場合や事前情報を活用したい場合 → ベイズ統計が有利
✅ 大規模データの解析や、シンプルな仮説検定 → 頻度主義統計が適切
Q2. ベイズ推定の事前分布はどのように選べばよい?
A. 事前分布の選び方には、次の2つのアプローチがあります。
-
非情報的事前分布(Uninformative Prior)
- できるだけデータに依存した推定を行いたい場合
- 例:一様分布 Beta(1,1) を使用
-
情報的事前分布(Informative Prior)
- 過去のデータや専門知識を考慮したい場合
- 例:過去の成功率が約 70% なら Beta(7,3)を使用
🔹 事前情報がない場合は一様分布や Jeffreys 事前分布を選択するとよい。
Q3. MCMC(マルコフ連鎖モンテカルロ法)を使うのはなぜ?
A. 事後分布を解析的に求めることが難しい場合に、MCMCを使って近似的にサンプルを生成し、分布を推定するため です。
✅ MCMCの主な手法
- Gibbs Sampling(変数ごとに条件付き分布をサンプリング)
- Metropolis-Hastings法(提案分布を用いてサンプルを生成)
MCMCを使うことで、複雑なベイズモデルでも事後分布を求めることができる ため、近年の機械学習や統計分析で広く活用されています。
Q4. ベイズ統計はどんな分野で活用されているの?
A. ベイズ統計は、次のような分野で幅広く活用されています。
✅ 医療分野:検査結果をもとに病気の確率を推定
✅ マーケティング:顧客の行動パターンを分析し、最適な広告を提示
✅ 機械学習:ナイーブベイズ分類器、ベイズ最適化など
✅ 金融:株価の変動予測、リスク評価
✅ 品質管理:不良品の発生率の推定
ベイズ統計は、「確率の更新」を活用することで、新しいデータが得られるたびに最適な推論ができる という利点があります。
5. まとめ
本記事では、ベイズ統計学について基礎から応用、Rでの実装まで詳しく解説しました。
✅ ベイズ統計のポイント
- 確率を「信念の更新」として扱う
- 事前確率・尤度・事後確率を考慮して推定を行う
- Rを使ってベイズ推定を実装できる
- MCMCを活用することで複雑なモデルの推定が可能
ベイズ統計が適している場面
- 医療の診断確率の推定
- マーケティングの顧客行動分析
- 機械学習・AIの意思決定
- 金融・経済データの分析
頻度主義統計とは異なる視点で確率を扱うベイズ統計は、近年ますます重要性が高まっています。
本記事を参考に、ぜひ実際のデータでベイズ統計を試してみてください!










