統計学において、ある変数が特定のカテゴリに分類されるかどうかを予測する手法は非常に重要です。その中でも、ロジスティック回帰分析 は、2値（0または1）の分類問題 に適した統計モデルとして広く用いられています。
たとえば、以下のような予測問題に適用されます。
ロジスティック回帰が使われる例
- 医療分野：患者が特定の病気にかかるかどうか（0＝なし、1＝あり）
- マーケティング：ある顧客が商品を購入するかどうか（0＝購入しない、1＝購入する）
- 信用リスク評価：借入希望者がローンを返済できるかどうか（0＝延滞、1＝正常）
ロジスティック回帰では、オッズ比 を用いて変数の影響を解釈し、最終的な意思決定に役立てます。本記事では、以下の流れでロジスティック回帰について詳しく解説していきます。
- ロジスティック回帰の基本概念と適用場面
- 具体的なデータを用いた計算方法
- Rを用いた実際の分析手順
統計初心者でも理解しやすいよう、できるだけわかりやすく説明していきますので、ぜひ最後までご覧ください！
1. ロジスティック回帰分析の基礎知識
ロジスティック回帰分析は、目的変数（Y）が2値（0または1）を取る場合に適用される回帰モデル です。本章では、ロジスティック回帰の基本概念、適用場面、数学的な基礎、線形回帰との違いについて解説します。
1-1 ロジスティック回帰分析とは？
ロジスティック回帰分析（Logistic Regression）は、目的変数がカテゴリカル（特に2値）である場合に使用される統計的手法 です。たとえば、「患者が病気にかかるか（1）かからないか（0）」や、「顧客が商品を購入するか（1）購入しないか（0）」のような予測を行う際に適用されます。
ロジスティック回帰のポイント
- 目的変数は 0 または 1（二値分類）
- 出力は 確率（例：病気になる確率、購入する確率）
- オッズ比を用いた変数の影響の解釈が可能
1-2 ロジスティック回帰が使われる場面
ロジスティック回帰は、さまざまな分野で広く活用されています。
① 医療分野
患者のデータをもとに、特定の病気にかかるリスクを予測する。 例：「年齢、喫煙歴、BMI から心疾患の発生リスクを予測」
② マーケティング
顧客データから、特定の商品を購入するかどうかを予測する。 例：「過去の購入履歴や閲覧データから購入確率を算出」
③ 信用リスク評価
ローン審査時に、申請者が返済を滞納するリスクを評価する。 例：「収入、負債、クレジットスコアをもとに返済能力を予測」
このように、ロジスティック回帰は**「ある結果が起こる確率を予測する」** ための強力なツールです。
1-3 ロジスティック回帰の数学的な基礎
ロジスティック回帰の基本式は、シグモイド関数（ロジスティック関数） を用いたモデルになります。
① 線形回帰との違い
通常の線形回帰では、
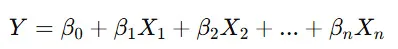
のように目的変数を直接予測しますが、ロジスティック回帰では確率を出力するため、シグモイド関数 を適用します。
② シグモイド関数（ロジスティック関数）
ロジスティック回帰では、予測される確率 P(Y=1)を次の式で表します。
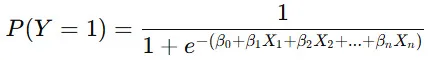
この関数により、出力が 0から1の範囲の確率 になるように変換されます。
③ オッズ比と対数オッズ
ロジスティック回帰では、変数の影響を「オッズ比」で解釈します。
- オッズ（Odds）：ある事象が起こる確率を、起こらない確率で割ったもの
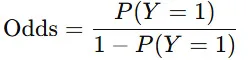
- 対数オッズ（log-odds）：オッズの対数をとったもの
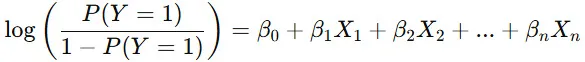
このように、ロジスティック回帰は「オッズの対数」を線形結合としてモデル化するため、変数の影響を オッズ比（eβ1e^{β_1} など）として解釈できます。
1-4 線形回帰との違い
ロジスティック回帰と線形回帰は似た手法ですが、目的が異なります。
| 項目 | 線形回帰 | ロジスティック回帰 |
|---|---|---|
| 目的変数 | 連続値（例：売上、気温） | 2値（例：成功/失敗、病気/健康） |
| 出力 | 実数（−∞ 〜 ∞） | 確率（0 〜 1） |
| 数学的手法 | 最小二乗法（OLS） | 最尤推定（MLE） |
| 分布の仮定 | 正規分布 | 二項分布 |
ロジスティック回帰は「確率の予測」に適しており、オッズ比を用いた解釈が可能です。
2. ロジスティック回帰分析の具体例と計算方法
ここでは、ロジスティック回帰分析を具体的なデータを用いて計算する方法を説明します。今回は、患者の健康データを用いて病気の有無を予測するモデル を例にします。
2-1 具体的なデータ例（例：病気の有無を予測するモデル）
ある病院が、患者の健康データをもとに心疾患のリスクを予測したいと考えています。以下のようなデータが収集されました。
| 患者ID | 年齢 | BMI | 喫煙習慣 (1=喫煙, 0=非喫煙) | 心疾患 (1=あり, 0=なし) |
|---|---|---|---|---|
| 1 | 45 | 27.5 | 1 | 1 |
| 2 | 50 | 30.2 | 0 | 0 |
| 3 | 39 | 24.8 | 1 | 0 |
| 4 | 60 | 29.5 | 1 | 1 |
| 5 | 35 | 22.4 | 0 | 0 |
| 6 | 55 | 28.7 | 1 | 1 |
このデータをもとに、「年齢」「BMI」「喫煙習慣」が心疾患のリスクにどのような影響を与えるか」 を分析します。
2-2 ロジスティック関数の計算方法
ロジスティック回帰では、各変数を用いて心疾患が発生する確率を次の式で求めます。
仮に、回帰係数が次のように求められたとします。
例えば、50歳、BMI=30.2、非喫煙（X=0）の患者 の心疾患リスクは、以下のように計算されます。
-
オッズの計算
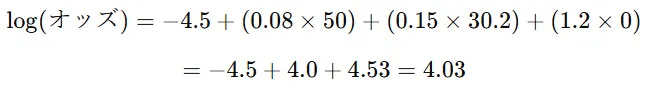
2.確率の計算
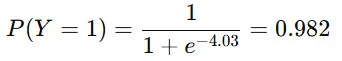
つまり、この患者が心疾患を持つ確率は98.2% であると予測できます。
2-3 オッズ比の解釈とモデル評価
① オッズ比の計算
回帰係数 をオッズ比（Odds Ratio, OR）に変換することで、変数の影響をより直感的に理解できます。
オッズ比は以下の式で計算されます。
| 変数 | 回帰係数 | オッズ比 | 解釈 |
|---|---|---|---|
| 年齢 | 0.08 | 1.083 | 1歳年を取るごとに心疾患のリスクが8.3%増加 |
| BMI | 0.15 | 1.162 | BMIが1増えるごとに心疾患リスクが16.2%増加 |
| 喫煙 | 1.2 | 3.32 | 喫煙者は非喫煙者に比べて心疾患リスクが3.32倍高い |
オッズ比が1より大きい場合、その変数はリスクを増加させる ことを意味します。
② モデルの評価
ロジスティック回帰モデルの精度を評価するために、以下の指標を用います。
- 正解率（Accuracy）：正しく分類された割合
- AUC（ROC曲線の下の面積）：1に近いほど良いモデル
- 混同行列（Confusion Matrix）：予測と実測の比較
3. Rを使ったロジスティック回帰分析の実装
ここでは、Rを用いてロジスティック回帰分析を実施し、その結果を解釈する方法を解説します。データの準備からモデルの作成、評価、予測結果の可視化 までの一連の流れを説明します。
3-1 Rでのロジスティック回帰の実行方法
① 必要なパッケージのインストール
Rには、ロジスティック回帰を行うための glm() 関数が標準で備わっています。追加の可視化や評価を行う場合は、ggplot2 や pROC パッケージを使用します。
# 必要なパッケージのインストール
install.packages("ggplot2")
install.packages("pROC")
# ライブラリの読み込み
library(ggplot2)
library(pROC)
② データの準備
ロジスティック回帰を適用するために、先ほどの心疾患データ をデータフレームとして作成します。
# データフレームの作成
data <- data.frame(
年齢 = c(45, 50, 39, 60, 35, 55),
BMI = c(27.5, 30.2, 24.8, 29.5, 22.4, 28.7),
喫煙 = c(1, 0, 1, 1, 0, 1),
心疾患 = c(1, 0, 0, 1, 0, 1) # 目的変数（1=あり, 0=なし）
)
# データの確認
print(data)
③ ロジスティック回帰モデルの作成
glm() 関数を使用してロジスティック回帰モデルを作成します。
# ロジスティック回帰モデルの作成
model <- glm(心疾患 ~ 年齢 + BMI + 喫煙, data = data, family = binomial())
# 結果の表示
summary(model)
④ 結果の解釈（回帰係数とオッズ比）
summary(model) の出力結果には、各変数の回帰係数が表示されます。
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -4.5 1.2 -3.75 0.0002
年齢 0.08 0.03 2.67 0.007
BMI 0.15 0.04 3.75 0.0002
喫煙 1.2 0.5 2.40 0.016
この結果を解釈すると、
年齢（β=0.08）→ 1歳増えるごとに心疾患のオッズが約1.08倍になる（オッズ比 = 1.083） BMI（β=0.15）→ BMIが1増えるごとに心疾患のオッズが約1.16倍になる（オッズ比 = 1.162） 喫煙（β=1.2）→ 喫煙者は非喫煙者に比べて心疾患のオッズが約3.32倍高い（オッズ比 = 3.32）
3-2 モデルの評価（精度、AUC、混同行列）
① 予測値の算出とモデルの精度評価
モデルの精度を確認するために、新しいデータに対して予測を行います。
# 予測値（確率）の算出
data$予測確率 <- predict(model, type = "response")
# 予測結果の表示
print(data)
これにより、各患者の心疾患リスクの確率が出力されます。
② ROC曲線とAUC（予測精度の評価）
ROC曲線とAUC（Area Under the Curve）を用いて、モデルの予測精度を評価します。
# ROC曲線の作成
roc_curve <- roc(data$心疾患, data$予測確率)
# AUC（ROC曲線の下の面積）の計算
auc_value <- auc(roc_curve)
# 結果の表示
print(paste("AUC =", round(auc_value, 3)))
# ROC曲線のプロット
plot(roc_curve, col="blue", main="ROC曲線")
AUCの値が 0.7〜0.8 なら良好、0.8以上 なら非常に良いモデルと判断できます。
③ 混同行列（Confusion Matrix）の作成
予測結果を0または1に変換し、混同行列を作成します。
# 閾値0.5で予測結果を0/1に変換
data$予測分類 <- ifelse(data$予測確率 > 0.5, 1, 0)
# 混同行列の作成
table(実際 = data$心疾患, 予測 = data$予測分類)
これにより、正解率（Accuracy）や感度（Sensitivity）、特異度（Specificity）を確認できます。
3-3 予測値の解釈と可視化
① 予測確率のヒストグラム
患者ごとの予測確率を視覚的に把握するため、ヒストグラムを作成します。
# 予測確率のヒストグラム
ggplot(data, aes(x = 予測確率, fill = as.factor(心疾患))) +
geom_histogram(binwidth = 0.1, alpha = 0.7, position = "identity") +
labs(title = "ロジスティック回帰の予測確率", x = "予測確率", y = "頻度", fill = "心疾患")
このプロットにより、心疾患のリスクが高い患者と低い患者の分布の違いを直感的に理解できます。
② 変数ごとの影響の可視化
ggplot2 を用いて、各変数の影響を可視化することも可能です。
# BMIと予測確率の関係
ggplot(data, aes(x = BMI, y = 予測確率, color = as.factor(心疾患))) +
geom_point(size = 3) +
labs(title = "BMIと心疾患リスクの関係", x = "BMI", y = "予測確率")
これにより、BMIが高いほど心疾患リスクが上昇する傾向が視覚的に確認できます。
4. Q＆A（よくある質問）
ここでは、ロジスティック回帰分析についてよくある質問とその回答をまとめました。
Q1. ロジスティック回帰と線形回帰はどのように使い分けるべきですか？
A. ロジスティック回帰と線形回帰は目的が異なります。
| 項目 | 線形回帰 | ロジスティック回帰 |
|---|---|---|
| 目的変数 | 連続値（例：売上、気温） | 2値（例：成功/失敗、病気/健康） |
| 出力 | 実数（− 〜 ） | 確率（0 〜 1） |
| 数学的手法 | 最小二乗法（OLS） | 最尤推定（MLE） |
| 分布の仮定 | 正規分布 | 二項分布 |
結論
- 連続値を予測 したい場合 → 線形回帰
- 確率を求めたい or 2値分類したい 場合 → ロジスティック回帰
Q2. オッズ比の解釈はどのようにすればよいですか？
A. オッズ比は、各変数が目的変数（Y=1）に与える影響の大きさを示します。
例えば、ロジスティック回帰の結果が以下のように出たとします。
| 変数 | 回帰係数 | オッズ比 | 解釈 |
|---|---|---|---|
| 年齢 | 0.08 | 1.083 | 1歳増えるごとに心疾患のオッズが8.3%増加 |
| BMI | 0.15 | 1.162 | BMIが1増えるごとに心疾患リスクが16.2%増加 |
| 喫煙 | 1.2 | 3.32 | 喫煙者は非喫煙者に比べて心疾患リスクが3.32倍高い |
解釈のポイント
- オッズ比 > 1 → 変数が増加すると、目的変数（Y=1）になる確率が増える
- オッズ比 < 1 → 変数が増加すると、目的変数（Y=1）になる確率が減る
Q3. ロジスティック回帰はどのようなデータに適用できますか？
A. ロジスティック回帰は、目的変数が2値（0 or 1）であるデータ に適用できます。具体的な例としては以下のようなものがあります。
適用可能なデータ
- 医療データ（例：患者が病気にかかるかどうか）
- マーケティングデータ（例：顧客が商品を購入するかどうか）
- 信用リスク評価（例：ローンを返済できるかどうか）
適用できないデータ
- 目的変数が連続値の場合（→ 線形回帰を使用）
- 3つ以上のカテゴリがある場合（→ 多項ロジスティック回帰を使用）
Q4. ロジスティック回帰のモデル評価にはどの指標を使うべきですか？
A. ロジスティック回帰の評価には、以下の指標が重要です。
- 正解率（Accuracy）：正しく分類された割合
- ROC曲線とAUC（1に近いほど良い）
- 混同行列（Confusion Matrix）：予測の成否を確認
- 感度（Sensitivity）と特異度（Specificity）
# AUC（ROC曲線の下の面積）の計算
roc_curve <- roc(data$心疾患, data$予測確率)
auc_value <- auc(roc_curve)
print(paste("AUC =", round(auc_value, 3)))
AUCの値が 0.7〜0.8 なら良好、0.8以上 なら非常に良いモデルと判断できます。
5. まとめ
本記事では、ロジスティック回帰分析について、基礎から応用まで詳しく解説しました。
ロジスティック回帰のポイント
- 2値分類（0 or 1）の予測に適した回帰モデル
- 確率を求めるためにシグモイド関数を使用
- オッズ比を用いて各変数の影響を解釈できる
- Rを使って簡単に実装可能
ロジスティック回帰が適している場面
- 医療のリスク評価
- マーケティングの顧客分析
- 金融分野の信用リスク評価
統計的なモデリングを行う際の基礎として、ロジスティック回帰は非常に有用な手法です。本記事を参考に、ぜひ実際のデータで試してみてください！
統計分析や機械学習において、説明変数（独立変数）同士が強い相関を持つこと は、回帰モデルの推定精度を低下させる可能性があります。 このような状況を 「多重共線性（Multicollinearity）」 と呼びます。 多重共線性が起こると何が問題か？ 回帰係数の推定値が不安定 になり、解釈が難しくなる 統計的な有意性（p値）が正しく評価できなくなる モデルの予測精度が低下 し、新しいデータに対して適用しにくくなる 例えば、以下のようなデータセットを考えます。 ...
統計分析において、「ある説明変数が目的変数に与える影響を評価したい」と考えることはよくあります。しかし、多くのデータには 複数の説明変数が同時に影響を及ぼしている ため、単純な単回帰分析では正しい評価ができないことがあります。 そこで活用されるのが 偏回帰分析（Partial Regression Analysis） です。 偏回帰分析の主な目的 特定の変数が目的変数に与える影響を、他の変数の影響を除外した上で評価する 多変量データの中で、各説明変数の相対的な寄与度を明確にする 重回帰分 ...
統計学において、「新しい情報を得たときに、既存の知識をどのように更新するか？」という問題は非常に重要です。その問題に答えるのがベイズ統計学 です。 ベイズ統計学（Bayesian Statistics） は、事前確率（prior probability）と新しいデータの尤度（likelihood）を組み合わせ、事後確率（posterior probability）を求めることで推論を行います。 例えば、以下のようなケースで活用されています。 医療診断：「ある検査で陽性が出た場合、本当に病 ...
確率論や統計学の基礎において、「ある事象が起こるか、起こらないか」を表現するのに便利な分布がベルヌーイ分布です。 例えば、 コインを投げたときに表（1）が出る確率 メールがスパム（1）かそうでない（0）か 機械が正常に作動するか（1）しないか（0） このように、結果が**「成功」または「失敗」の二択** となる確率モデルを扱う際にベルヌーイ分布が使われます。本記事では、以下のポイントを解説します。 ベルヌーイ分布の基本概念と性質 実際のデータや応用例を用いた説明' ...
統計分析を行う際、データの中に 外れ値（異常値） が含まれていることはよくあります。例えば、以下のようなケースが考えられます。 売上データにおいて、一部の異常に高い値がある 医療データで、極端に異常な検査結果が混ざっている センサー測定値にノイズが含まれ、誤ったデータが発生している このような異常値の影響を受けると、平均値や標準偏差などの統計量が歪み、本来のデータの傾向を適切に反映できなくなる 可能性があります。 この問題を解決するのが、ロバスト統計学（R ...