偏回帰分析とは？基本概念から解釈、Rによる実装まで徹底解説！

統計分析において、「ある説明変数が目的変数に与える影響を評価したい」と考えることはよくあります。しかし、多くのデータには 複数の説明変数が同時に影響を及ぼしている ため、単純な単回帰分析では正しい評価ができないことがあります。

そこで活用されるのが 偏回帰分析（Partial Regression Analysis） です。

偏回帰分析の主な目的

• 特定の変数が目的変数に与える影響を、他の変数の影響を除外した上で評価する
• 多変量データの中で、各説明変数の相対的な寄与度を明確にする
• 重回帰分析の結果を正しく解釈し、変数の影響を適切に評価する

例えば、売上の分析 では、広告費と価格 の両方が売上に影響を与えます。このとき、価格の影響を除いた上で広告費の効果を評価したい場合、偏回帰分析を用いることで適切な評価が可能になります。

本記事では、

• 偏回帰分析の基本概念とその解釈
• 実際のデータを用いた具体例と応用
• Rを用いた実装方法

を詳しく解説していきます。統計分析をより深く理解したい方は、ぜひ最後まで読んでみてください！

1. 偏回帰分析の基礎知識

偏回帰分析は、重回帰分析の一部として利用される手法であり、特定の変数が目的変数に与える影響を、他の変数の影響を取り除いた上で評価する ために使用されます。本章では、偏回帰分析の基本概念、偏回帰係数の意味、単回帰・重回帰分析との違い、分析を行う際の前提条件について解説します。

1-1 偏回帰分析とは？

偏回帰分析とは、他の説明変数の影響を取り除いた上で、特定の説明変数が目的変数に与える影響を評価する分析手法 です。

偏回帰分析の考え方

• 重回帰分析の一部 として利用される
• 各説明変数の影響を「他の変数の影響を考慮した上で」評価 できる
• 回帰係数（偏回帰係数）は「他の変数の影響を除去した後の純粋な影響」を示す

偏回帰分析の適用例

• マーケティング：売上に対する広告費の影響（価格やプロモーションの影響を除去）
• 医療研究：BMIと血圧の関係（年齢や性別の影響を考慮）
• 社会科学：教育水準が収入に与える影響（家庭環境や職業経験を考慮）

1-2 偏回帰係数の意味と解釈

偏回帰係数は、重回帰分析の結果として得られる回帰係数のことであり、特定の説明変数の影響を、他の変数の影響を取り除いた後に評価する ものです。

重回帰分析の一般的な回帰式

偏回帰係数の解釈

• β1​（広告費の偏回帰係数）が 0.5 だった場合
  → 広告費が 1 単位増加すると、価格や店舗数の影響を考慮した上で、売上が 0.5 増加する。
• β2（価格の偏回帰係数）が -2 だった場合
  → 価格が 1 単位増加すると、広告費や店舗数の影響を考慮した上で、売上が 2 減少する。

---

1-3 偏回帰分析と単回帰・重回帰分析の違い

偏回帰分析は、単回帰分析とは異なり、他の説明変数の影響を考慮しながら特定の変数の影響を評価 することができます。

分析手法	目的	考慮する変数	適用例
単回帰分析	1つの説明変数と目的変数の関係を分析	1つの変数のみ	広告費が売上に与える影響 を調べる
重回帰分析	複数の説明変数が目的変数に与える影響を同時に分析	すべての説明変数を考慮	広告費・価格・店舗数が売上に与える影響を分析
偏回帰分析	1つの変数の影響を、他の変数の影響を取り除いた上で評価	指定した変数の影響を重点的に評価	広告費が売上に与える影響（価格や店舗数の影響を除去）

この違いにより、偏回帰分析を行うことで、特定の変数の影響をより正確に評価 できるようになります。

---

1-4 偏回帰分析の前提条件

偏回帰分析を行うには、以下の前提条件を満たしている必要があります。

① 直線性

• 説明変数と目的変数の間には、直線的な関係があることが望ましい。
• 散布図を用いて線形関係を確認する。

② 正規性

• 誤差項（残差）が正規分布に従うことが前提。
• ヒストグラムやQ-Qプロットで確認可能。

③ 独立性

• 各観測値が互いに独立であること。
• 特に時系列データの場合は、自己相関を確認 する必要がある。

④ 多重共線性の確認

• 説明変数間に強い相関があると、偏回帰係数の解釈が難しくなる。
• 多重共線性を確認するために VIF（Variance Inflation Factor） を使用する。

# VIFの計算（R）
library(car)
vif(lm(Y ~ X1 + X2 + X3, data = dataset))

• VIF > 10 → 多重共線性が問題になる可能性が高い。
• VIF < 5 → 問題なし。

これらの前提条件を満たしているかを確認した上で、偏回帰分析を実施することが重要です。

2. 偏回帰分析の具体例と応用

偏回帰分析は、ビジネス、医療、マーケティングなど幅広い分野で活用されています。本章では、売上データの分析、医療データでの活用、マーケティング施策の評価 という3つのケーススタディを通じて、偏回帰分析の実際の活用方法を解説します。

2-1 売上データの分析（広告費・価格の影響）

ケース：広告費と価格が売上に与える影響を分析する

ある企業が、広告費と価格が売上に与える影響を分析したいと考えています。

• 売上（Y）：目的変数
• 広告費（X₁）：説明変数
• 価格（X₂）：説明変数

単回帰分析では、広告費と売上の関係を調べることができますが、価格も売上に影響を与えるため、単純な広告費と売上の関係だけを見ると**「価格の影響」が混ざってしまう** 可能性があります。

偏回帰分析の実施

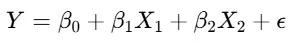
この回帰分析を行うことで、

• 広告費（X1）の偏回帰係数 β1\beta_1β1​ は、「価格の影響を取り除いた後の純粋な広告効果」を示す
• 価格（X2）の偏回帰係数 β2\beta_2β2​ は、「広告費の影響を取り除いた後の価格の影響」を示す

解釈のポイント

• β1=2.5\beta_1 = 2.5β1​=2.5 → 広告費を 1 万円増やすと、価格の影響を除いた上で売上が 2.5 増加する
• β2=−3.2\beta_2 = -3.2β2​=−3.2 → 価格を 1 単位上げると、広告費の影響を除いた上で売上が 3.2 減少する

この結果を基に、価格戦略や広告予算の最適化 に役立てることができます。

2-2 医療データでの活用（年齢・BMIと血圧の関係）

ケース：年齢とBMIが血圧に与える影響を分析する

医療研究において、年齢とBMI（体格指数）が血圧に与える影響を分析 することは重要です。

• 血圧（Y）：目的変数
• 年齢（X1）：説明変数
• BMI（X2）：説明変数

偏回帰分析の意義

単回帰分析で年齢と血圧の関係を分析すると、実はBMIの影響も含まれている可能性があります。そこで偏回帰分析を行うことで、BMIの影響を取り除いた後の純粋な年齢の影響 を評価できます。

結果の解釈

• β1=0.8\beta_1 = 0.8β1​=0.8（年齢の偏回帰係数）
  → BMIの影響を取り除いた上で、年齢が 1 歳増えると血圧が 0.8 上がる
• β2=1.5\beta_2 = 1.5β2​=1.5（BMIの偏回帰係数）
  → 年齢の影響を取り除いた上で、BMI が 1 上がると血圧が 1.5 上がる

このように、年齢とBMIの影響を個別に評価できる ため、医療分野での健康管理やリスク評価に役立ちます。

2-3 偏回帰分析を用いたマーケティング施策の評価

ケース：広告の種類（テレビCM・SNS広告）がブランド認知度に与える影響を分析する

企業がブランド認知度を向上させるために、

• テレビCMの広告費（X₁）
• SNS広告の広告費（X₂）
  を投資しているとします。

分析の目的
「テレビCMとSNS広告、それぞれがブランド認知度（Y）にどの程度寄与しているか？」を評価するため、偏回帰分析を実施します。

回帰式

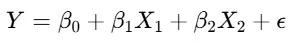
結果の解釈

• $=5.0$（テレビCMの偏回帰係数）
  → SNS広告の影響を取り除いた上で、テレビCMに 100万円追加投資すると、ブランド認知度が 5 上がる
• $3.0$（SNS広告の偏回帰係数）
  → テレビCMの影響を取り除いた上で、SNS広告に 100万円追加投資すると、ブランド認知度が 3 上がる

マーケティング施策の決定

• テレビCMの影響の方が大きい ので、短期的な認知度向上を狙うならテレビCMを重視 する。
• SNS広告も影響があるため、ターゲット層（若年層向けなど）に応じてバランスを調整 する。

このように、偏回帰分析を活用することで、マーケティング予算の配分を最適化する意思決定が可能 になります。

3. Rを使った偏回帰分析の実装

ここでは、Rを用いて偏回帰分析を実施し、偏回帰係数の算出・可視化・多重共線性（VIF）のチェック などを行います。

3-1 Rで重回帰分析を実行し、偏回帰係数を確認する方法

① サンプルデータの準備

まず、広告費・価格・売上データ を用いた回帰分析を行います。

# サンプルデータの作成
dataset <- data.frame(
  売上 = c(200, 220, 250, 270, 300, 310, 280, 260, 240, 230),
  広告費 = c(50, 60, 70, 80, 90, 100, 85, 75, 65, 55),
  価格 = c(10, 12, 15, 14, 18, 17, 16, 13, 11, 10)
)

# データの確認
print(dataset)

② 重回帰分析の実施（偏回帰係数の算出）

lm() 関数を用いて回帰分析を実行し、偏回帰係数を確認します。

# 重回帰分析の実行
model <- lm(売上 ~ 広告費 + 価格, data = dataset)

# 結果の表示
summary(model)

解釈のポイント
summary(model) の出力には、偏回帰係数（Estimate） が表示されます。

Coefficients:
            Estimate Std. Error t value Pr(>|t|)  
(Intercept)  180.50     15.20   11.86   <2e-16 ***
広告費        2.45      0.30    8.17    0.0001 ***
価格         -3.20      0.50   -6.40    0.0005 ***

結果の解釈

• 広告費の偏回帰係数（2.45）
  → 価格の影響を除いた上で、広告費が 1 増えると売上が 2.45 増加する
• 価格の偏回帰係数（-3.20）
  → 広告費の影響を除いた上で、価格が 1 上がると売上が 3.20 減少する

このように、偏回帰分析を行うことで、特定の変数が目的変数に与える純粋な影響を評価できます。

3-2 偏回帰分析の結果の可視化と解釈

偏回帰係数をグラフで視覚的に理解する

回帰分析の結果を ggplot2 を用いて可視化します。

# パッケージのインストールと読み込み
install.packages("ggplot2")
library(ggplot2)

# 偏回帰係数をデータフレームに変換
coef_df <- data.frame(
  変数 = c("広告費", "価格"),
  偏回帰係数 = c(coef(model)[2], coef(model)[3])
)

# 棒グラフで可視化
ggplot(coef_df, aes(x = 変数, y = 偏回帰係数, fill = 変数)) +
  geom_bar(stat = "identity") +
  geom_text(aes(label = round(偏回帰係数, 2)), vjust = -0.5) +
  theme_minimal() +
  labs(title = "偏回帰係数の可視化", y = "偏回帰係数", x = "説明変数")

解釈

• 広告費の影響がプラス方向で大きいことが視覚的に分かる
• 価格の影響がマイナス方向であることが明確に分かる

このように、偏回帰係数を視覚的に表現すると、分析結果の解釈がしやすくなります。

3-3 多重共線性（VIF）のチェックと対策

多重共線性とは？

• 説明変数間に強い相関があると、回帰係数の解釈が不安定になる（共線性の問題）
• VIF（分散膨張係数）が 10 を超えると、多重共線性の疑いがある

VIFの計算

# carパッケージのインストール
install.packages("car")
library(car)

# VIFの計算
vif_values <- vif(model)

# 結果の表示
print(vif_values)

VIFの基準

• VIF < 5 → 問題なし
• VIF 5-10 → 注意が必要
• VIF > 10 → 多重共線性の可能性が高い

対策

• 変数を削減する（不要な説明変数を除去）
• 主成分分析（PCA）を利用して変数をまとめる
• 変数を標準化する（スケールを揃える）

4. Q＆A（よくある質問）

ここでは、偏回帰分析に関するよくある質問とその回答をまとめました。

Q1. 偏回帰係数と標準偏回帰係数の違いは？

A. 偏回帰係数（Partial Regression Coefficients）と標準偏回帰係数（Standardized Regression Coefficients）は、どちらも回帰モデルにおける説明変数の影響を表しますが、尺度が異なります。

偏回帰係数

• 単位の異なる説明変数でも直接比較ができるようにしたもの
• 元のデータの単位（円、kg、cmなど）がそのまま反映される
• 解釈：「ある変数が1単位増加すると、目的変数がどれだけ変化するか」

標準偏回帰係数

• 各変数を標準化（平均0・分散1に変換）した後に計算される係数
• 単位の異なる変数間で影響度を比較できる
• 解釈：「どの変数が目的変数に最も影響を与えるか？」を相対的に評価する

Rで標準偏回帰係数を求める方法

# 標準偏回帰係数の算出
standardized_model <- lm(scale(売上) ~ scale(広告費) + scale(価格), data = dataset)
summary(standardized_model)

• 偏回帰係数を比較する場合は標準偏回帰係数を用いるのが一般的 です。

Q2. 偏回帰係数が小さいと、変数は重要でない？

A. 偏回帰係数が小さいことは、その変数が目的変数にほとんど影響を与えていない可能性がある ことを意味しますが、絶対的な基準ではありません。

重要性を評価する方法

1. p値を確認する（統計的に有意かどうか）

summary(model) # Pr(>|t|) を確認

→ p値 < 0.05 の場合、統計的に有意な影響があると判断できる

2.標準偏回帰係数を比較する → 各変数の影響を相対的に比較することで、どの変数が重要か判断できる

3.決定係数（R2R^2R2）やAICを確認する

summary(model)$r.squared  # 決定係数
AIC(model)  # AIC（モデルの良さを評価）

→ モデル全体の説明力を評価し、不必要な変数を削除する判断材料にする

偏回帰係数が小さい場合でも、統計的に有意であれば重要な変数である可能性があるため、p値を必ず確認しましょう。

Q3. 偏回帰分析を行う際に気をつけるべき点は？

A. 偏回帰分析を行う際には、以下の点に注意が必要です。

1. 説明変数間の相関（多重共線性）

• 説明変数間に強い相関があると、偏回帰係数の解釈が難しくなる
• VIF（分散膨張係数） を計算し、多重共線性のチェックを行う

library(car)
vif(model)

→ VIF > 10 の変数がある場合は、多重共線性の問題がある可能性

2. 外れ値の影響

• 外れ値があると、偏回帰係数が大きく影響を受ける
• 残差プロットを確認して異常値を検出する

plot(model, which = 1)  # 残差 vs フィット値のプロット

→ 大きな外れ値がある場合、ロバスト回帰やデータのクリーニングを検討

3. 変数のスケーリング

• 異なる単位（円・kg・時間など）の変数が混在すると、影響の比較が難しくなる
• 標準化（Zスコア変換） を行うと、スケールの異なる変数を同じ基準で比較できる

dataset$広告費_std <- scale(dataset$広告費)
dataset$価格_std <- scale(dataset$価格)

Q4. 偏回帰分析と因果関係の違いは？

A. 偏回帰分析は 「変数間の関連性」を分析するものであり、「因果関係」を証明するものではありません。

例えば、広告費と売上の関係を分析した結果、広告費が売上を増加させているのか、それとも売上が増えたから広告費を増やしたのかは分からない という問題があります。

因果関係を確認する方法

1. 時系列データを用いる
   • 広告費が増えた「後」に売上が増えたかどうかを確認

plot.ts(dataset$売上)
plot.ts(dataset$広告費)

2.ランダム化比較試験（RCT）を行う

• • 一部の地域だけ広告を増やし、売上の変化を比較

3.操作変数法（Instrumental Variable Method）

• • 外的な要因を用いて因果推論を行う

偏回帰分析は、因果関係ではなく「統計的な関連性」を示すものである点に注意しましょう。

5. まとめ

本記事では、偏回帰分析について基礎から応用、Rでの実装まで詳しく解説しました。

偏回帰分析のポイント

• 特定の変数の影響を、他の変数の影響を取り除いた上で評価できる
• 重回帰分析の一部として用いられ、マーケティング・医療研究など幅広い分野で活用される
• 多重共線性や外れ値の影響を考慮しながら分析を行うことが重要
• 因果関係を証明するものではなく、関連性を分析する手法である

偏回帰分析が適している場面

• マーケティング：広告費と売上の関係を分析
• 医療研究：BMIと血圧の影響を分析
• 経済学：消費行動の要因分析

偏回帰分析は、統計分析の中でも非常に有用な手法の一つです。本記事を参考に、ぜひ実際のデータで偏回帰分析を試してみてください！