はじめに
LASSO回帰(らっそかいき)は、機械学習でよく用いられる線形回帰モデルの一種です。LASSO回帰は、過学習を防ぎ、モデルの解釈性を高めるという特徴を持ちます。近年、データ分析や予測モデル構築において、LASSO回帰は非常に重要な役割を果たしています。
このブログ記事では、R言語を用いたLASSO回帰の実践的な方法を解説します。初学者の方でも理解しやすいように、基礎的な説明から具体的な操作手順まで、丁寧に説明していきます。
L1正則化とは?
L1正則化は、損失関数に対して係数の絶対値の和を加えることにより、一部の係数をゼロにすることを目指す正則化手法です。この特性により、無関係または重要でない特徴をモデルから除外することができ、結果としてよりシンプルで解釈しやすいモデルを生成します。
L1正則化を含む損失関数は通常、以下のように表されます
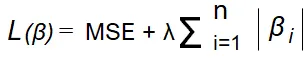
ここで、MSE は平均二乗誤差、β はモデルの係数、λは正則化の強度を調整するパラメータです。パラメータ λの値が大きいほど、多くの係数がゼロになります。
L1正則化の利点
- 特徴選択: 自動的に無関係な特徴を削除し、モデルをシンプルにします。
- 多重共線性の対処: 相関の高い変数が存在する場合でも、一部の変数のみを選択して他を無視します。
- 解釈の容易さ: 生成されたスパースなモデルは、どの変数が予測に重要かを理解しやすくします。
R言語でのL1正則化の実装例
R言語でL1正則化を適用するには、前述したようにglmnetパッケージが最も一般的です。
以下に簡単な例を示します。
install.packages("glmnet") #パッケージのインストールがまだの場合
library(glmnet)
# データ生成
set.seed(101)
X <- matrix(rnorm(100 * 20), nrow = 100, ncol = 20)
beta <- runif(20, min = -2, max = 2)
y <- X %*% beta + rnorm(100, sd = 0.5)
# L1正則化を用いたモデルフィッティング
fit <- glmnet(X, y, alpha = 1)
# 係数の確認
print(coef(fit))
スクリプトの解説
ライブラリの読み込み: glmnet パッケージを読み込んでいます。このパッケージは、リニアおよびロジスティック回帰モデルにL1正則化(ラッソ)やL2正則化(リッジ)を適用するための関数を提供します。
乱数シードの設定: set.seed() 関数は乱数の生成に使われるシードを設定します。これにより、コードを実行するたびに同じ乱数が生成され、結果が再現可能になります
set.seed(101):乱数生成のシードを設定し、結果の再現性を保証します。
X <- matrix(rnorm(100 * 20), nrow = 100, ncol = 20):100個の観測値と20個の特徴を持つデータ行列を生成します。ここで、rnorm(100 * 20) は標準正規分布からランダムな数値を生成します。
beta <- runif(20, min = -2, max = 2):20個の係数を、-2から2の範囲で一様分布からランダムに生成します。
y <- X %*% beta + rnorm(100, sd = 0.5):生成した係数betaと説明変数Xを用いて応答変数yを計算します。このモデルには、0.5の標準偏差を持つ正規分布のノイズを加えます。
fit <- glmnet(x, y, alpha = 1):L1正則化(ラッソ回帰)を使用してモデルをフィットします。ここで、xとyはそれぞれ説明変数と応答変数です。alpha = 1はラッソ回帰を指定しています。print(coef(fit)):フィットされたモデルの係数を表示します。coef()関数はモデルの係数を抽出し、print()関数でこれをコンソールに出力します。ラッソ回帰では、多くの係数がゼロになる可能性があります。これは、ラッソ回帰が特徴選択を行いながら回帰を実行するためです。
結果の解釈の仕方
上記スクリプトを実行した結果は、glmnetでフィットされたL1正則化(ラッソ)モデルの係数を示しています。ここで、異なる正則化パラメータ(ラムダ)の値に対応し、各行が異なる予測変数(V1からV20)の係数です。また、「Intercept」は切片(モデルの定数項)を示しています。
解釈のポイント:
-
スパース性(係数がゼロになる):
- L1正則化の主な特徴は、不要な係数をゼロにすることでモデルをスパースにする能力です。この表で多くの
.(ドット)が見られるのは、その係数がゼロになっていることを意味します。例えば、V1、V2、V5、V6、V9などの変数は多くの場合で係数がゼロです。
- L1正則化の主な特徴は、不要な係数をゼロにすることでモデルをスパースにする能力です。この表で多くの
-
係数の変化:
- ラムダの値が小さくなるにつれて(左から右へ)、係数の絶対値が増加することが多いです。これは、ラムダが小さいと正則化の影響が減少し、より多くの係数がモデルに「生き残る」ことを意味します。
-
重要な予測変数の識別:
- 係数がゼロでない変数(例えば、V3、V4、V7、V8、V10)は、モデルがその予測において重要だと判断している変数です。これらの変数の係数は、予測変数が目的変数に与える影響の大きさと方向を表します。
-
ラムダの選択:
- 実際のモデリングでは、過剰適合を避けつつ最も予測性能の高いラムダの値を選択することが重要です。これは通常、交差検証を使用して決定されます。ここでは、61個の異なるラムダ値に対するモデルが示されていますが、どのラムダが最適かはデータに依存します。
-
プロットの利用:
plot(fit)を使用すると、ラムダに対する各係数の経路(パス)が描かれ、どの変数がどのラムダ値でモデルに入ったり出たりするかを視覚的に確認できます。これはモデル選択の際に非常に有益です。
この表から、どの予測変数が目的変数に影響を与える可能性が高いか、またその影響の強さと方向を把握することができます。また、多くの予測変数がモデルから省略されていることから、データセット内の情報の冗長性や不要な特徴を省くことに成功しているとも言えます。
交差検証機能を使ったLASSO回帰のやり方
実際のモデリングで最適なラムダの値を選択するために、glmnet パッケージで提供されている交差検証機能を使用する方法について詳しく解説します。交差検証は、モデルの一般化能力を評価し、過学習を防ぐために非常に有効な手段です。
交差検証の基本
交差検証では、データセットを複数のサブセット(通常は「フォールド」と呼ばれます)に分割し、それぞれのフォールドを一度ずつテストセットとして使用し、残りのフォールドを訓練セットとして使用します。このプロセスを繰り返し、各フォールドに対するモデルのパフォーマンスを評価します。これにより、特定のデータセットに過度に適合することなく、モデルのパフォーマンスをより公平に評価することが可能になります。
R言語での交差検証実装方法
# ライブラリのロード
library(glmnet)
# データの生成
set.seed(101)
X <- matrix(rnorm(100 * 20), nrow = 100, ncol = 20)
beta <- runif(20, min = -2, max = 2)
y <- X %*% beta + rnorm(100, sd = 0.5)
# 交差検証を用いたLASSOモデルのフィッティング
cv_fit <- cv.glmnet(X, y, alpha = 1, type.measure="mse", nfolds = 10)
# 交差検証の結果のプロット
plot(cv_fit, main="LASSO Cross-Validation Plot")
# lambda.min に対する赤い点線の追加
abline(v=log(cv_fit$lambda.min), col="red", lwd=2, lty=2)
# lambda.1se に対する青い点線の追加
abline(v=log(cv_fit$lambda.1se), col="blue", lwd=2, lty=2)
スクリプトの解説
このスクリプトは、R言語を使用してLASSO回帰(L1正則化を含む線形回帰モデル)を適用し、その性能を交差検証で評価する一連のプロセスを示しています。具体的には、データの生成からモデルのフィッティング、そして結果の可視化までを含んでいます。以下、スクリプトの各部分について詳しく解説します。
glmnetライブラリをロードします。このライブラリは、LASSO回帰やリッジ回帰など、正則化を含む線形モデルを実装するための関数を提供しています。
set.seed(101)で乱数のシードを設定し、結果の再現性を保証します。
Xは100行20列の行列で、各要素は標準正規分布から生成されます。これが説明変数(特徴量)です。
betaは20個の係数で、各係数は-2から2の範囲の一様分布から生成されます。これらは各説明変数の真の係数です。
yは応答変数で、線形結合 X %*% beta に標準偏差0.5の正規分布ノイズを加えたものです。
cv.glmnetは、指定されたデータにLASSOモデルをフィッティングし、交差検証を通じてその性能を評価します。
alpha = 1はLASSO回帰を指定しています(alpha = 0はリッジ、0 < alpha < 1はエラスティックネット回帰)。
type.measure="mse"は性能評価の基準として平均二乗誤差(MSE)を使用することを指定します。
nfolds = 10はデータを10分割して交差検証を行うことを指定します。
plot関数により、LASSOモデルの交差検証結果がプロットされます。このプロットは、様々なラムダ値におけるMSEを示し、どのラムダ値が最適かを視覚的に評価するのに役立ちます。
abline関数を使用して、プロット上に特定のラムダ値を示す線を追加します。lambda.minはMSEが最小となるラムダの値、lambda.1seは最小MSEの1標準誤差以内で最も単純なモデルを提供するラムダの値です。
log(cv_fit$lambda.min)とlog(cv_fit$lambda.1se)で、ラムダ値の対数を取っています(プロットが対数スケールの場合)。
colで線の色を指定し(赤と青)、lwdで線の太さ、ltyで線のスタイル(点線)を指定しています。
結果の解釈の仕方
先ほどのスクリプトを実行すると次のようなプロットが得られます。
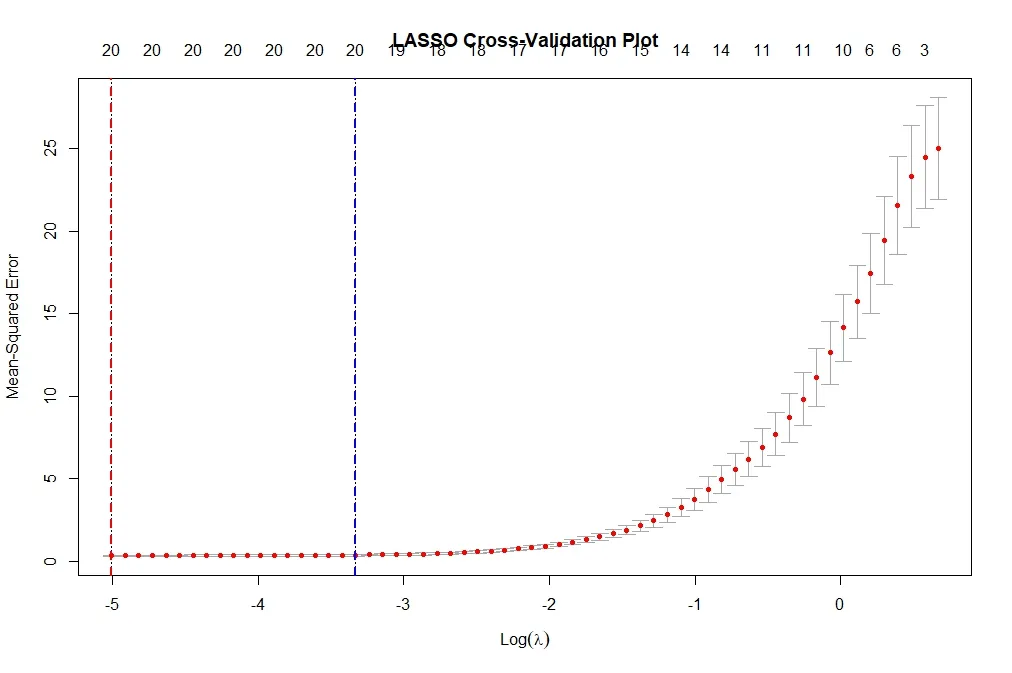
LASSO回帰におけるlambda.min(赤い点線)とlambda.1se(青い点線)の選択は、モデルの予測性能と複雑性(または疎性)のトレードオフを考慮する必要があります。ここでの選択は、データの特性、モデルの目的、および過学習のリスクへの対応に基づいて行われます。
lambda.min(赤い点線)
- 定義: このラムダ値は、交差検証で得られた平均二乗誤差(MSE)が最小になる点です。
- 利点: このラムダ値を選択すると、交差検証に基づいて最も良い予測精度を持つモデルを得ることができます。つまり、このラムダでフィットしたモデルは、利用可能なデータに最も適合するモデルです。
- 欠点: 最小のMSEを追求することは、特にデータセットが小さいまたは変数が多い場合に過学習(overfitting)を引き起こす可能性があります。過学習したモデルは新しい未知のデータに対してうまく一般化できないかもしれません。
lambda.1se(青い点線)
- 定義: このラムダ値は、最小MSEに1標準誤差を加えたときのラムダ値であり、これを選択すると少し性能は落ちるものの、より単純で堅牢なモデルを得ることができます。
- 利点:
lambda.1seはモデルをより単純化し、過学習のリスクを減らします。このラムダ値でのモデルは、必要以上に複雑になることなく、データの基本的なパターンを捉えることができるため、新しいデータや外部のサンプルに対してもうまく機能する可能性が高いです。 - 欠点: 予測精度がわずかに低下する可能性がありますが、これは過学習を避けるためのトレードオフです。
選択基準
どちらのラムダ値を選択するかは、モデリングの目的に強く依存します。以下に一般的な指針を示します:
- 予測性能の最大化が重要な場合(たとえば、競争やパフォーマンスが最も重視される状況):
lambda.minを選択します。 - モデルの解釈性や一般化が重要な場合(たとえば、新しいデータに対する予測が求められる場合や、モデルの結果を説明する必要がある場合):
lambda.1seを選択します。
最終的に、これらの選択は、特定のデータとモデルの使用状況に基づいて慎重に検討されるべきです。また、異なるラムダ値におけるモデルのパフォーマンスを評価するために追加の検証やテストを行うことも一般的です。










