Rのggplot2パッケージで積み上げ棒グラフを作成する方法を解説します。積み上げ棒グラフは、データの分布や比較を視覚的にわかりやすく表示するグラフの一種です。例えば、商品の売上ランキングや、アンケート結果の集計結果などを、積み上げ棒グラフで表示することで、一目で全体像を把握することができます。
本記事では、Rのggplot2パッケージを使用して、積み上げ棒グラフを作成する方法を解説します。
具体的にはエクセルファイルデータをＲで読み込んで、積み上げ棒グラフで作成する場合を例に手順を解説していきます。
また、ggplot2の基本的な機能を解説しながら、積み上げ棒グラフのカスタマイズ方法についても説明します。
エクセルデータの準備
以下のような、日本の産業別実質GDPの推移のエクセルデータを用意しました。
Rで読み込んでいくのは青色のセルのみ読み込んでいきます。詳しくは以前のブログ記事を参考にしてください。
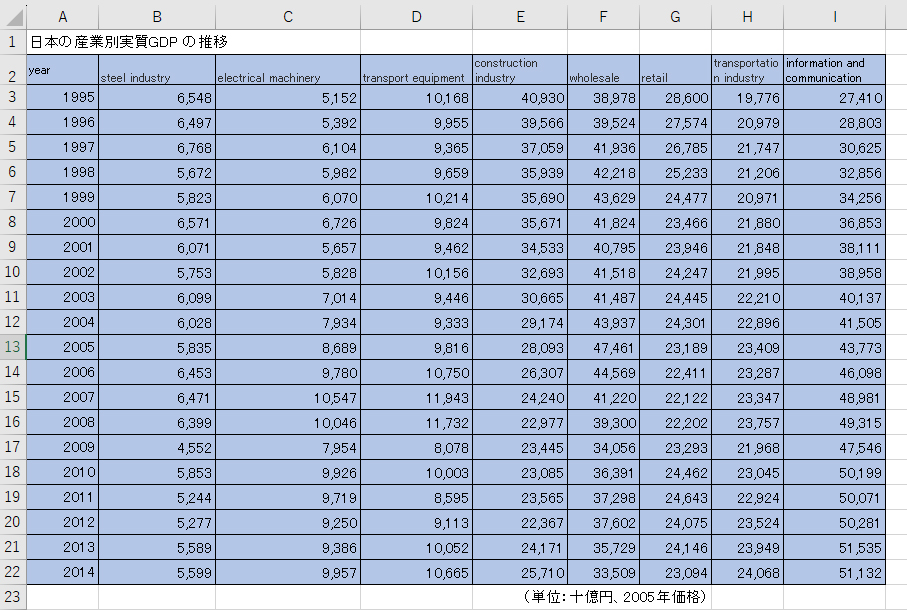
青色のセルを読み込むスクリプトは次のとおりです。
library(readxl)
# Excelファイルのパス(ご自身のファイル名と場所に書き換えてください)
file_path <- "F:/ブログ用/17R/関数辞典/04 read_excel/GDP.xlsx"
# read_excel関数のオプションを設定してデータフレームを読み込む
df <- read_excel(
path = file_path,
sheet = "Sheet3", # シート名
range = "A2:I22", # 読み込む範囲
col_types = c("text", rep("numeric",8)), # 列のデータ型を指定
na = "NA", # 欠損値として扱う文字列
skip = 1, # 最初の1行をスキップ
n_max = 50 # 読み込む最大行数
)Rでdfを開いてみましょう。
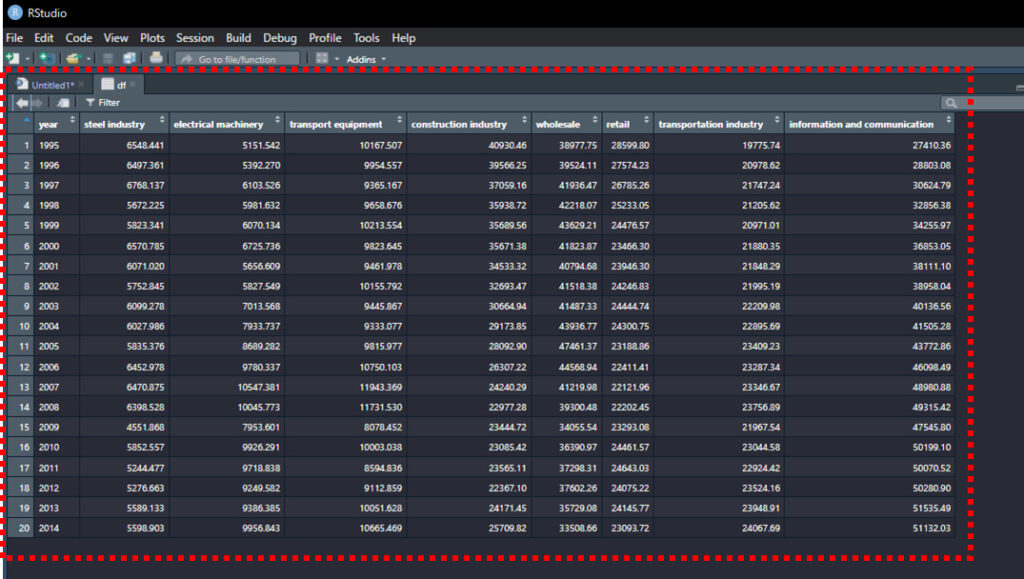
エクセルファイルをRに読み込めているのが確認できました。
積み上げ棒グラフの作成
既にExcelファイルからデータフレーム(df)を読み込んでいるので、ここから各年度ごとに2列目から9列目のデータを積み上げた棒グラフを作成するスクリプトを書きます。以下にスクリプトを示します。
install.packages("tidyr") #インストールされていない人は入れてください
library(tidyr)
library(ggplot2)
# データを長い形式に変換
df_long <- gather(df, key = "Year", value = "Value", -year)
# 積み上げ棒グラフの作成
ggplot(df_long, aes(x = year, y = Value, fill = Year)) +
geom_bar(stat = "identity", position = "stack") +
theme_minimal() +
labs(x = "年", y = "値", fill = "カテゴリー") +
theme(
axis.text.x = element_text(angle = 45, hjust = 1, size = 12, family = "Helvetica", face = "bold"), # X軸のラベルと数値のフォント
axis.title.x = element_text(size = 12, family = "Helvetica", face = "bold"), # X軸タイトルのフォントサイズ
axis.title.y = element_text(size = 12, family = "Helvetica", face = "bold"), # Y軸タイトルのフォントサイズ
axis.text.y = element_text(size = 12, family = "Helvetica", face = "bold") # Y軸数値のフォント
)
生成されるグラフは次のとおりです。
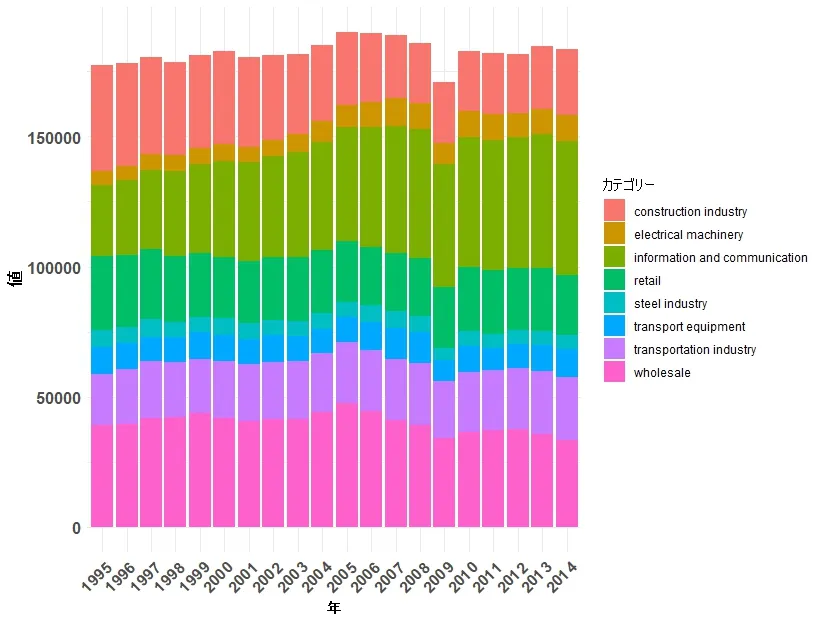
・gather(df, key = "Year", value = "Value", -SampleName)
これによりデータを長い形式に変換しています。言葉で説明するより実際にdf_longをRで見てみます。
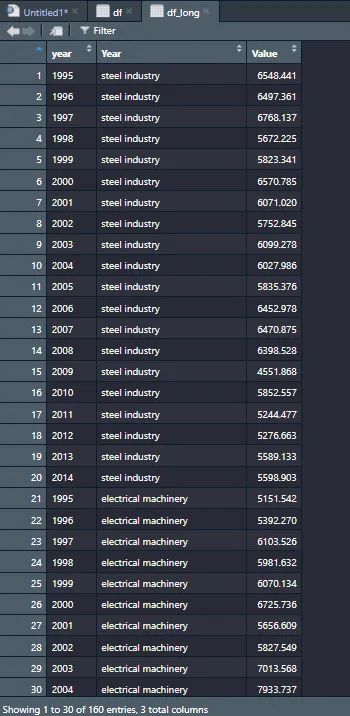
分かりましたでしょうか？
gather関数を使用してデータを長い形式に変換する理由は？
gather関数を使用してデータを長い形式に変換する理由は、ggplot2でのグラフ作成に適したデータ形式にするためです。具体的には、以下の理由があります。
-
ggplot2のデータ要件:ggplot2は、データを「長い形式」（long format）で扱うことを前提としています。長い形式では、各行が単一の観測値を表し、各列が異なる変数を表します。これにより、複数の変数間の関係をより明確に表現できます。 -
変数の区別: 元のデータフレームでは、各年度のデータが異なる列に格納されています。
gatherを使用すると、これらの列が2つの新しい列（この場合はYearとValue）に統合されます。これにより、年度ごとのデータが一つの列にまとめられ、もう一つの列にはそれに対応する値が格納されます。 -
グラフ作成の柔軟性: 長い形式に変換することで、
ggplot2を使用してさまざまな種類のグラフを簡単に作成できます。特に積み上げ棒グラフの場合、各棒のセグメント（この場合は年度）をfill属性に割り当てることが容易になります。
具体的に、gather関数のこの使用例では以下のことが行われています：
df：変換するデータフレーム。key = "Year"：新しく作成される列で、元のデータフレームの列名（年度）が格納されます。value = "Value"：新しく作成されるもう一つの列で、元のデータフレームの値が格納されます。-year：この部分は、year列を除いて他のすべての列をYearとValueに変換することを意味します。
この変換により、元の「幅広い形式」（wide format）のデータフレームが、ggplot2でのグラフ作成に適した「長い形式」に変換されます。
スクリプトの解説(# 積み上げ棒グラフの作成)
-
ggplot(df_long, aes(x = SampleName, y = Value, fill = Year)):ggplot(df_long, ...)：ggplot2を使用してグラフを作成します。ここでdf_longは、データが長い形式に変換されたデータフレームです。aes(x = SampleName, y = Value, fill = Year)：aesはエステティック（視覚的属性）を設定します。x = SampleName：X軸にはSampleName列のデータを使用します。y = Value：Y軸にはValue列のデータを使用します。fill = Year：棒グラフの色分けにYear列のデータを使用します。これにより、異なる年度のデータが異なる色で表示されます。
-
geom_bar(stat = "identity", position = "stack"):geom_bar(...)：棒グラフを作成します。stat = "identity"：データの値をそのまま棒の高さとして使用します。position = "stack"：棒を積み上げる形式で表示します。これにより、各サンプル名に対して、異なる年度のデータが積み上げられた棒グラフが作成されます。
-
theme_minimal():- グラフのテーマをミニマル（シンプルなデザイン）に設定します。
-
labs(x = "サンプル名", y = "値", fill = "年度"):- 軸ラベルや凡例のタイトルを設定します。
x = "サンプル名"：X軸のラベルを「サンプル名」とします。y = "値"：Y軸のラベルを「値」とします。fill = "年度"：凡例のタイトルを「年度」とします。
-
theme(axis.text.x = element～)):- この部分で、軸のテキストとタイトルの見た目をカスタマイズしています。
axis.text.x: X軸のテキスト（数値やカテゴリ）のフォントスタイルを設定します。角度を45度にし、フォントサイズ、フォントファミリー（Helvetica）、フォントスタイル（太字）を指定しています。axis.title.xとaxis.title.y: X軸とY軸のタイトルのフォントスタイルを設定します。axis.text.y: Y軸のテキストのフォントスタイルを設定します。
色を指定するには？
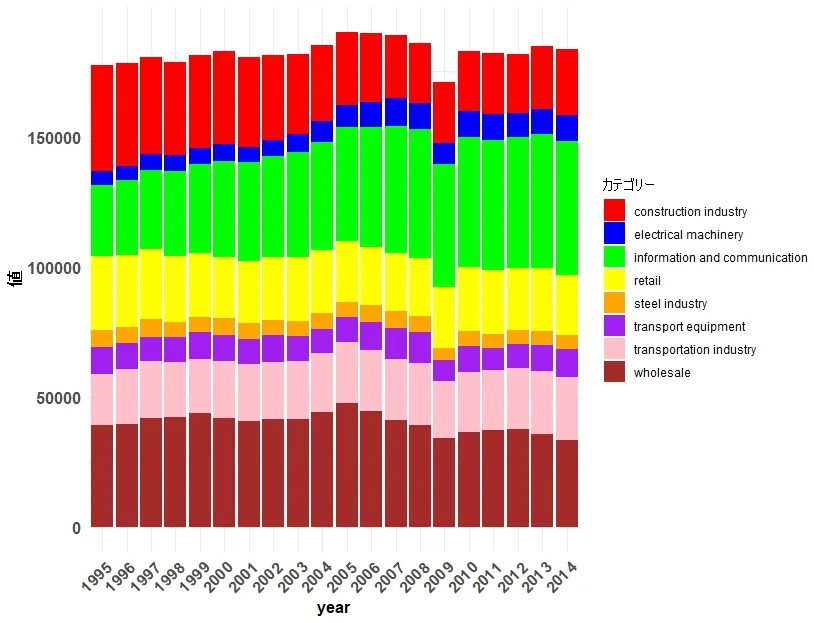
積み上げ棒グラフで特定の色を指定するには、scale_fill_manual関数を使用して、fillエステティックに対して色をマッピングします。以下は、あなたのスクリプトを修正したものです。ここでは、Yearごとに異なる色を指定しています。色はご自身の好みに合わせて変更してください。
# 積み上げ棒グラフの作成
ggplot(df_long, aes(x = year, y = Value, fill = Year)) +
geom_bar(stat = "identity", position = "stack") +
scale_fill_manual(values = c("red", "blue", "green", "yellow", "orange", "purple", "pink", "brown", "grey")) + # ここで色を指定
theme_minimal() +
labs(x = "year", y = "値", fill = "カテゴリー") +
theme(
axis.text.x = element_text(angle = 45, hjust = 1, size = 12, family = "Helvetica", face = "bold"), # X軸のラベルと数値のフォント
axis.title.x = element_text(size = 12, family = "Helvetica", face = "bold"), # X軸タイトルのフォントサイズ
axis.title.y = element_text(size = 12, family = "Helvetica", face = "bold"), # Y軸タイトルのフォントサイズ
axis.text.y = element_text(size = 12, family = "Helvetica", face = "bold") # Y軸数値のフォント
)このスクリプトによって次のようなグラフになります。
統計分析や機械学習において、説明変数（独立変数）同士が強い相関を持つこと は、回帰モデルの推定精度を低下させる可能性があります。 このような状況を 「多重共線性（Multicollinearity）」 と呼びます。 多重共線性が起こると何が問題か？ 
回帰係数の推定値が不安定 になり、解釈が難しくなる 統計的な有意性（p値）が正しく評価できなくなる モデルの予測精度が低下 し、新しいデータに対して適用しにくくなる 例えば、以下のようなデータセットを考えます。 ...
統計分析において、「ある説明変数が目的変数に与える影響を評価したい」と考えることはよくあります。しかし、多くのデータには 複数の説明変数が同時に影響を及ぼしている ため、単純な単回帰分析では正しい評価ができないことがあります。 そこで活用されるのが 偏回帰分析（Partial Regression Analysis） です。 偏回帰分析の主な目的 特定の変数が目的変数に与える影響を、他の変数の影響を除外した上で評価する 多変量データの中で、各説明変数の相対的な寄与度を明確にする 重回帰分 ...
統計学において、「新しい情報を得たときに、既存の知識をどのように更新するか？」という問題は非常に重要です。その問題に答えるのがベイズ統計学 です。 ベイズ統計学（Bayesian Statistics） は、事前確率（prior probability）と新しいデータの尤度（likelihood）を組み合わせ、事後確率（posterior probability）を求めることで推論を行います。 例えば、以下のようなケースで活用されています。 医療診断：「ある検査で陽性が出た場合、本当に病 ...
数学や物理、経済学、機械学習の分野では、「偏微分」という概念が頻繁に登場します。 例えば、以下のような場面で偏微分が活用されます。 物理学：物体の運動を記述する方程式（速度や加速度）を導く 経済学：利潤最大化やコスト最小化の最適化問題を解く 機械学習：ニューラルネットワークの学習アルゴリズム（勾配降下法）に利用 では、偏微分とは何なのか？どのように計算すればよいのか？本記事では、偏微分の基礎から応用までを詳しく解説 していきます！ 1. 偏微分の基礎知識 ...
統計分析や機械学習において、説明変数（独立変数）同士が強い相関を持つこと は、回帰モデルの推定精度を低下させる可能性があります。 このような状況を 「多重共線性（Multicollinearity）」 と呼びます。 多重共線性が起こると何が問題か？ 回帰係数の推定値が不安定 になり、解釈が難しくなる 統計的な有意性（p値）が正しく評価できなくなる モデルの予測精度が低下 し、新しいデータに対して適用しにくくなる 例えば、以下のようなデータセットを考えます。 ...
統計分析において、「ある説明変数が目的変数に与える影響を評価したい」と考えることはよくあります。しかし、多くのデータには 複数の説明変数が同時に影響を及ぼしている ため、単純な単回帰分析では正しい評価ができないことがあります。 そこで活用されるのが 偏回帰分析（Partial Regression Analysis） です。 偏回帰分析の主な目的 特定の変数が目的変数に与える影響を、他の変数の影響を除外した上で評価する 多変量データの中で、各説明変数の相対的な寄与度を明確にする 重回帰分 ...