こんにちは!今日は、統計学において非常に重要な概念である「ピアソンの相関係数」について深掘りしていきます。この記事を読むことで、相関係数の意味や計算方法を理解する手助けになれば嬉しいです。
1. ピアソンの相関係数とは?
ピアソンの相関係数は、2つの数量変数間の線形的な関係の強さと方向を評価する統計的な手法です。この「線形的な関係」というのは、一方の変数が増加(または減少)すると、もう一方の変数も一定の割合で増加(または減少)する関係を指します。
相関係数の値は、-1から1までの範囲で変動します。この値の絶対値が大きいほど、2つの変数間の線形関係の強さが強いことを示します。具体的には:
- +1の場合: 2つの変数間に完全な正の線形関係が存在します。一方の変数が増加すると、もう一方の変数も増加します。
- 0の場合: 2つの変数間に線形関係はありません。一方の変数の変動は、もう一方の変数の変動とは関係がないことを示します。
- -1の場合: 2つの変数間に完全な負の線形関係が存在します。一方の変数が増加すると、もう一方の変数は減少します。
このように、相関係数は2つの変数の関係性を数値で示すためのものですが、重要な点として、それが因果関係を意味するわけではないということを理解しておく必要があります。たとえ相関関係が強いとしても、一方の変数がもう一方の変数の原因であるとは断定できないのです。
2. なぜピアソンの相関係数が必要なのか?
ピアソンの相関係数の重要性は、データの関係性を定量的に評価することにあります。実際の研究やビジネスの場面で、2つの変数間に何らかの関連性があるかどうかを知ることは非常に価値があります。以下は、ピアソンの相関係数が必要とされるいくつかの理由です:
-
データの傾向の確認:初めて目にするデータセットにおいて、2つの変数間に関係性があるかどうかの初歩的な分析として利用されます。例えば、気温とアイスクリームの売上の関係性を見る場面などで、相関係数を計算することで大まかな傾向を掴むことができます。
-
変数選択の際の参考:複数の変数を持つデータ分析の際、どの変数をモデルに取り入れるかを決める基準として、相関係数が利用されることがあります。高い相関を持つ変数が複数ある場合、多重共線性の問題が生じる可能性があるため、変数選択の際の参考として使われます。
-
仮説検証:研究やビジネスの場面で、ある変数と別の変数の間に関連性があるという仮説が立てられた場合、この仮説の妥当性を確認するために相関係数を計算します。相関係数が高ければ仮説の支持が得られる可能性が高まります。
-
効果的な意思決定:ビジネスの場面で、ある施策の影響を他の指標と関連付けて評価する際に、相関係数を用いることで、施策の効果をより具体的に把握することが可能となります。
以上のように、ピアソンの相関係数は、データの関連性を明確にし、より賢明な意思決定や研究の方向性を導くための鍵となるツールとして利用されます。
3. ピアソンの相関係数の計算方法
ピアソンの相関係数の計算には、特定の数式を用いますが、実際に計算を進める前に、その背後にある概念や各項目がどのような意味を持つのかを理解することが大切です。以下で数式の詳細を深堀りします。
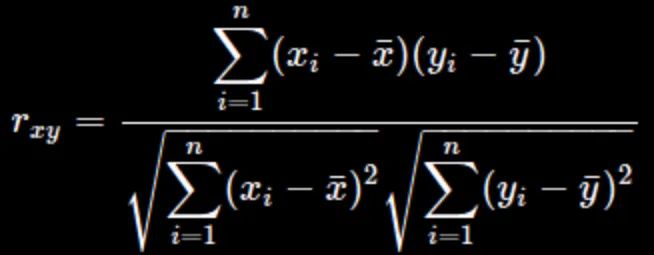
この式における各項目の説明:
:これが求めたいピアソンの相関係数です。
:データの総数です。例えば、10人の学生のテストスコアを比較する場合、 は10となります。
この式を分解して考えると、分子は2つの変数の共分散を示しており、分母は各変数の分散の平方根を掛け合わせたものです。相関係数は、共変動を標準化したものとして理解できます。そのため、値が-1から1の間に収まるのです。
手計算での計算が可能ですが、実際の研究やビジネスの現場では、ExcelやR、Pythonなどのツールを使用して効率的に計算を行うことが一般的です。
4. 注意点
ピアソンの相関係数は非常に便利なツールである一方で、誤った解釈や利用方法をすると誤った結論を導くリスクがあります。以下に、ピアソンの相関係数を使用する際の主要な注意点を詳しく挙げます。
-
因果関係の誤解: 相関関係は因果関係を意味しないというのは基本中の基本ですが、これを忘れてしまうと大きな解釈の誤りを犯すことになります。たとえ2つの変数間に強い相関が見られたとしても、一方がもう一方の原因であるとは限りません。外部の第三の変数の影響や偶然の一致など、様々な要因が考えられます。
-
非線形の関係: ピアソンの相関係数は、2つの変数間の線形の関係のみを評価します。もし変数間に曲線的な関係(例: 二次関数や三次関数のような関係)がある場合、相関係数はその関係をうまく捉えられない場合があります。
-
外れ値の影響: データに外れ値が含まれている場合、相関係数はその影響を強く受けやすいです。外れ値によって相関係数が大きく変動する可能性があるため、データの前処理や確認をしっかり行うことが必要です。
-
変数の尺度: ピアソンの相関係数を計算する前に、変数の尺度や単位が適切であるかを確認することも重要です。異なる尺度や単位の変数をそのまま比較すると、意味のない結果を導く可能性があります。
-
データの数量: サンプルサイズが非常に小さい場合、得られた相関係数の信頼性が低くなる可能性があります。一方で、非常に大きなサンプルサイズでは、微小な関係性でも統計的に有意に見えてしまうことがあります。サンプルサイズと結果の解釈のバランスを取ることが大切です。
以上のように、ピアソンの相関係数を正確に活用するためには、その背後にある原理をしっかりと理解し、適切な判断と解釈を行うことが求められます。
まとめ
ピアソンの相関係数は、2つの変数間の線形関係の強さと方向を知るための強力なツールです。ただし、その解釈には注意が必要です。相関係数を上手く活用することで、データ分析の精度を高めることができます。

