Rで始めるRidge（リッジ）回帰：理論から実践まで【初心者向けガイド】

はじめに

リッジ回帰は線形回帰モデルの一種で、予測変数間の多重共線性を扱いやすくするために正則化項を導入します。この記事では、R言語を使用してリッジ回帰を行う方法を、理論の説明から具体的なコードの実行まで段階的に解説します。

リッジ回帰の基礎

リッジ回帰（Ridge Regression）は、回帰分析において共線性を緩和し、モデルの過学習を防ぐために導入される技法です。具体的には、損失関数にL2正則化項（係数の二乗の和）を加えることで、係数の絶対値を抑え、より一般化されたモデルを生成します。

データの生成

まず、Rでリッジ回帰を行うためのサンプルデータを生成します。ここでは100個のサンプルと20個の特徴を持つデータセットを作成します。

# ライブラリのロード
library(glmnet)

# データの生成
set.seed(101)
X <- matrix(rnorm(100 * 20), nrow = 100, ncol = 20)
beta <- runif(20, min = -2, max = 2)
y <- X %*% beta + rnorm(100, sd = 0.5)

リッジ回帰モデルのフィッティング

glmnetパッケージを使用してリッジ回帰を行います。リッジ回帰はalphaパラメータを0に設定することで実行できます。

# リッジ回帰モデルのフィッティング
fit <- glmnet(X, y, alpha = 0)

モデルの評価と係数の確認

フィットしたモデルの係数を確認し、どのように各特徴が応答変数に影響を与えるかを見てみましょう。

ラムダの選択

リッジ回帰において、ラムダ（正則化パラメータ）の選択はモデルの予測性能と複雑性のバランスを大きく左右します。適切なラムダの値を見つけるために、cv.glmnet 関数を用いて交差検証を行い、最適なラムダ値を定めます。

# 交差検証によるラムダの選択
cv_fit <- cv.glmnet(X, y, alpha = 0)
plot(cv_fit)

このプロットには複数のラムダ値に対するモデルの性能が示され、最適なラムダを選択するための指標が提供されます。特に、lambda.min（最小の交差検証誤差を与えるラムダ）とlambda.1se（最小誤差の1標準誤差範囲内で最も単純なモデルを提供するラムダ）は重要です。これらのラムダ値に対応する線をプロットに追加して、視覚的に理解しやすくします。

# lambda.min に対する赤い点線の追加
abline(v=log(cv_fit$lambda.min), col="red", lwd=2, lty=2)

# lambda.1se に対する青い点線の追加
abline(v=log(cv_fit$lambda.1se), col="blue", lwd=2, lty=2)

ここで、abline() 関数を用いて赤と青の点線を追加します。赤い線は lambda.min を、青い線は lambda.1se を示しており、これによりモデルの選択に役立つ視覚的な情報を提供します。これにより、過学習を避けつつ良好な予測精度を得るためのラムダの選択が容易になります。

まとめ

このセクションでは、リッジ回帰の適用において重要なラムダの選択方法を、実際のRコードを使って解説しました。赤と青の点線をプロットに追加することで、最適なラムダ値の選択を直感的に行うことができます。この手法により、データに最も適したリッジ回帰モデルを効果的に特定することが可能となります。

リッジ回帰とラッソ回帰の違い

リッジ回帰とラッソ回帰は、線形回帰モデルを拡張したもので、共に回帰係数にペナルティを加える正則化技術です。しかし、それぞれのアプローチには重要な違いがあります。これらの違いを理解することは、どのモデルをデータ分析に使用するかを決定する上で非常に重要です。

リッジ回帰（Ridge Regression）

正則化項: リッジ回帰は、係数の二乗の和に基づくL2正則化を使用します。具体的には、損失関数に

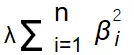
を加えます。ここで、 $λ$ は正則化パラメータで、 $β_{i}$ はモデル係数です。

特徴: すべての係数をゼロにはしないが、係数の値を小さくしてすべての変数をモデルに保持します。これにより、多重共線性の問題が軽減され、モデルの安定性が向上します。

使用場面: 特徴量が多く、互いに強い相関がある場合や、モデルの安定性と予測性能のバランスが重視される場合に適しています。

ラッソ回帰（Lasso Regression）

正則化項: ラッソ回帰は、係数の絶対値の和に基づくL1正則化を使用します。損失関数に

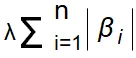
を加えます。

特徴: 一部の係数を完全にゼロにすることができます（スパース性）。この性質により、無関係または重要でない特徴を自動的にデータセットから除外する効果があります。これは事実上の変数選択メカニズムとして機能します。

使用場面: 変数の数が多く、その中から予測に有用な少数の変数を選び出したい場合や、モデルの解釈性を重視する場面で有効です。

リッジとラッソの選択基準

変数選択の必要性: ラッソは変数選択が可能なため、不要な特徴を取り除く必要がある場合に適しています。リッジはすべての変数をモデルに保持するため、変数選択は行われません。
パラメータの推定: リッジはゼロでない係数を生成しますが、ラッソは一部の係数を完全にゼロにできるため、より解釈しやすいモデルを生成することがあります。
予測性能と計算コスト: 両者は計算コストが異なり、モデルの予測性能にも差が出ることがあります。ラッソの方が計算コストが高い傾向がありますが、変数の数を減らすことでパフォーマンスが向上することもあります。

まとめ

リッジ回帰とラッソ回帰はそれぞれ異なる特性と利点を持ち、解析の目的やデータの特性に応じて適切なモデルを選択することが重要です。具体的な分析目的やデータの構造、予済み要求を考慮して、最も適切なアプローチを選ぶことが求められます。

回帰分析

2024/4/26

R言語で始めるRidge（リッジ）回帰：理論から実践まで【初心者向けガイド】

はじめにリッジ回帰は線形回帰モデルの一種で、予測変数間の多重共線性を扱いやすくするために正則化項を導入します。この記事では、R言語を使用してリッジ回帰を行う方法を、理論の説明から具体的なコードの実行まで段階的に解説します。リッジ回帰の基礎リッジ回帰（Ridge Regression）は、回帰分析において共線性を緩和し、モデルの過学習を防ぐために導入される技法です。具体的には、損失関数にL2正則化項（係数の二乗の和）を加えることで、係数の絶対値を抑え、より一般化されたモデルを生成します。データの生成 ...

回帰分析

2024/4/26

R言語でLASSO回帰（ラッソ回帰）をマスター！初心者でも理解できる実践ガイド

はじめに LASSO回帰（らっそかいき）は、機械学習でよく用いられる線形回帰モデルの一種です。LASSO回帰は、過学習を防ぎ、モデルの解釈性を高めるという特徴を持ちます。近年、データ分析や予測モデル構築において、LASSO回帰は非常に重要な役割を果たしています。このブログ記事では、R言語を用いたLASSO回帰の実践的な方法を解説します。初学者の方でも理解しやすいように、基礎的な説明から具体的な操作手順まで、丁寧に説明していきます。 L1正則化とは？ L1正則化は、損失関数に対して係数の絶対値の和を加える ...

回帰分析

2023/12/22

多重回帰分析とは？　複数の要因を同時に捉えるデータ分析手法

こんにちは！統計やデータ分析に関心がある方、あるいは業務でのデータ解析が求められている方に、多重回帰分析についての基本をご紹介します。簡単な言葉で説明していきますので、安心して読み進めてくださいね。 1. 回帰分析って何？まず、多重回帰分析を理解する前に、基本的な「回帰分析」とは何かを知ることが大切です。回帰分析とは、変数間の関係性を数学的にモデル化する手法です。主に、1つの目的変数と1つ以上の予測変数の間の関係を調べるために使用されます。例えば、家の価格（目的変数）が部屋の大きさ（予測変数）にどれ ...

回帰分析

2023/12/21

単回帰分析: 基本的な概念と計算

こんにちは！今日は統計の中の一つのトピック、「単純線形回帰」について詳しく学ぶことにします。統計学が少し難しく感じるかもしれませんが、ここで一緒に基本的な概念と計算方法を学べば、もう少し身近に感じることができるでしょう。 1. 単回帰分析とは？単回帰分析は、2つの変数間の関係を直線で表現するための統計的手法の一つです。一つの独立変数（説明変数）と一つの従属変数（目的変数）の関係を明らかにします。この関係を理解することで、一つの変数が変わると、もう一つの変数がどのように変動するのかを予測することができます ...

特殊なグラフ

2024/4/26

R言語でQQプロットを作成する方法

はじめに QQプロット（Quantile-Quantileプロット）は統計分析で非常に役立つツールです。これを使って、データセットが特定の理論分布に従っているかどうかを視覚的に評価することができます。R言語には、この種のプロットを簡単に作成できる強力なツールが用意されています。この記事では、R言語を使用してQQプロットを作成する基本的なステップを説明します。必要なパッケージ QQプロットを描くためには、基本的にstatsパッケージが必要ですが、これはRの標準パッケージに含まれているため、特別なインストー ...

グラフのカスタマイズ

2024/4/17

Rでエラーバー付きのグラフを作成する方法

はじめにデータの可視化において、エラーバーはデータの変動や不確実性を表現する重要な手段です。R言語を用いたグラフ作成においてエラーバーを追加する方法を学ぶことで、データの解釈をより深く行うことが可能になります。この記事では、基本的なエラーバーの追加方法から、カスタマイズする方法までを段階的に解説します。エラーバーを含むグラフの重要性エラーバーは、データ点のばらつきや測定の不確かさを表すのに役立ちます。科学研究や技術報告でよく見られるこの表現方法は、データの信頼性や有効性を視覚的に伝えるために不可欠で ...

グラフのカスタマイズ

2024/4/17

R言語でのグラフ作成：X軸とY軸のスケール比の設定方法

はじめに R言語はデータ分析と可視化に非常に強力なツールです。特にグラフ作成機能は多くのデータサイエンティストや研究者に利用されています。この記事では、R言語でグラフを作成する際にX軸とY軸のスケール比を設定する方法を詳しく解説します。スケール比を調整することで、データの比率や関係性をより正確に表現することが可能になります。グラフの基本的な作成方法まず、R言語で基本的なグラフを作成する方法から見ていきましょう。ここでは、plot() 関数を使用してシンプルな散布図を描きます。 # サンプルデータの生成 ...

特殊なグラフ

2024/4/18

R言語でバイオリンプロットを作成する方法：データの分布を視覚化

はじめにバイオリンプロットは箱ひげ図の概念を拡張したもので、データの分布密度も同時に表現できるグラフです。この記事では、R言語を用いてバイオリンプロットを作成する手順を、基本から応用まで丁寧に解説します。バイオリンプロットとは？バイオリンプロットは、データの確率密度を視覚的に表現する方法の一つで、中央値や四分位数といった統計量だけでなく、データの分布形状も示すことができます。これにより、データの全体的な傾向をより詳細に把握することが可能になります。 Rでバイオリンプロットを作成する Rでは、ggpl ...

グラフのカスタマイズ

2024/4/18

R言語で箱ひげ図に平均値を追加する方法

はじめに箱ひげ図はデータの分布、特に四分位数や極値を視覚的に表現する強力なツールですが、時には平均値を表示することでデータの理解をさらに深めることができます。この記事では、R言語を使用して箱ひげ図に平均値を追加する方法を解説します。箱ひげ図とは？箱ひげ図（Boxplot）は、データの中央値、四分位数、外れ値を表示し、データの分布を要約するのに役立ちます。しかし、平均値もまたデータの中心傾向を理解するのに重要な指標であり、これを箱ひげ図に追加することで、さらに多角的なデータ解析が可能になります。 Rで ...