統計学において、データの比較を行う手法は数多く存在します。その中でも、「フリードマン検定」は、対応のある3群以上のデータを比較するための非パラメトリックな方法です。本記事では、フリードマン検定の基本概念から具体例、Rを使った実装までを詳しく解説します。
フリードマン検定は、対応のあるデータに適用されるため、たとえば同じ被験者に対して異なる条件下でのテストを行う場合に有効です。例えば、ある食品メーカーが新しい3種類のレシピを開発し、同じパネリストに試食してもらった場合、それぞれの食品の評価に違いがあるかをフリードマン検定で確認できます。
本記事では、以下の流れでフリードマン検定を解説していきます。
- フリードマン検定の基本概念と適用場面
- 具体的なデータを使った計算方法
- Rを用いた実際の分析手順
統計学初心者でも理解できるよう、できるだけ分かりやすく解説していきますので、ぜひ最後まで読んでみてください!
1. フリードマン検定の基礎知識
フリードマン検定は、対応のある3群以上のデータを比較するための非パラメトリック検定です。この手法は、分散分析(ANOVA)のように正規分布の仮定を必要とせず、データの順位を用いるため、データが正規性を満たさない場合でも利用できます。本章では、フリードマン検定の概要、適用場面、前提条件、類似手法との比較について解説します。
1-1 フリードマン検定とは?
フリードマン検定(Friedman test)は、対応のある3つ以上の群の中央値に差があるかを判定する非パラメトリックな手法です。主に以下のような場合に適用されます。
- 同じ被験者に対して、複数の条件下で測定したデータを比較する場合
- 反復測定されたデータの差を検定したい場合
- 正規分布を仮定できないデータに対して、分散分析(ANOVA)の代替手法として利用する場合
フリードマン検定の基本的な流れ
- 各被験者ごとに測定されたデータを順位化する
- 各条件の平均順位を求める
- フリードマン検定の統計量を算出し、帰無仮説(全ての群に差がない)が棄却されるかを判定する
フリードマン検定では、対応のあるデータを順位に変換し、その順位の分布を分析するため、外れ値の影響を受けにくいという特徴があります。
1-2 フリードマン検定が使われる場面
フリードマン検定は、次のようなケースで利用されることが多いです。
① 医学・心理学分野での臨床試験
同じ被験者が異なる薬や治療法を試した場合の効果を比較するのに適しています。例えば、3種類の治療法A・B・Cの効果を同じ患者グループで測定し、それらの間に差があるかを検定する際に使用できます。
② 食品・嗜好調査
ある食品メーカーが3種類の新しい味のスナックを開発し、同じテスターに試食してもらった後、味の評価を順位付けして分析する場合にも適用できます。
③ 教育・学習効果の比較
同じ生徒が異なる学習方法(例:動画学習、対面授業、eラーニング)で学んだ後のテスト結果を比較するのに利用できます。
1-3 フリードマン検定の前提条件
フリードマン検定を使用する際には、以下の前提条件を満たしていることが重要です。
- データが対応のあるデータであること
- 同じ被験者(または同じグループ)から3回以上の測定が行われていること
- データが順序尺度または間隔尺度であること
- フリードマン検定では順位データを使用するため、数値データでなくても順位付けが可能なら適用できる
- 各被験者において全ての条件のデータが揃っていること(欠測値がないこと)
- 欠測値がある場合は、統計処理の前に適切に処理する必要がある
1-4 フリードマン検定と他の類似手法との比較(ANOVAとの違い)
フリードマン検定は、通常の分散分析(ANOVA)とは異なり、正規分布の仮定を必要としません。しかし、適用範囲が似ているため、どちらを使用すべきか迷うことがあります。以下の表で両者の違いを比較します。
| 項目 | フリードマン検定 | 反復測定ANOVA |
|---|---|---|
| データの種類 | 非パラメトリック(順位データ) | パラメトリック(数値データ) |
| 分布の仮定 | 正規分布の仮定なし | 正規分布が前提 |
| 使用目的 | データの中央値の差を比較 | データの平均値の差を比較 |
| 外れ値の影響 | 受けにくい | 受けやすい |
このように、フリードマン検定はデータの正規性を仮定しなくてよいため、柔軟に利用できるメリットがあります。しかし、単純な平均値の比較ではなく順位の比較になるため、データの特性に応じて適切な手法を選択することが重要です。
2. フリードマン検定の具体例と計算方法
フリードマン検定の基本概念を理解したところで、次は具体的なデータを用いた計算方法について詳しく説明します。本章では、食品の評価データを例に挙げ、フリードマン検定の手順をステップごとに解説していきます。
2-1 具体的なデータ例(例:3種類の食品の評価データ)
ここでは、ある食品メーカーが3種類の新しいレシピ(A、B、C)を開発し、同じ10人のテスターに試食してもらい、それぞれの食品に対して評価を行ったとします。
データの例(評価は1~10のスコアで記録)
| 被験者 | レシピA | レシピB | レシピC |
|---|---|---|---|
| 1 | 7 | 8 | 6 |
| 2 | 6 | 7 | 5 |
| 3 | 8 | 9 | 7 |
| 4 | 5 | 6 | 4 |
| 5 | 9 | 8 | 7 |
| 6 | 6 | 5 | 4 |
| 7 | 7 | 9 | 6 |
| 8 | 5 | 7 | 6 |
| 9 | 8 | 7 | 5 |
| 10 | 6 | 8 | 7 |
このように、各被験者が3つの異なるレシピを評価し、スコアをつけています。このデータをもとに、フリードマン検定を実施し、それぞれのレシピに統計的な有意な違いがあるかどうかを検証します。
2-2 フリードマン検定の計算手順
フリードマン検定の計算は、以下のステップで進められます。
① 各被験者ごとに順位を付ける
フリードマン検定では、評価スコアではなく順位を用いるため、各被験者ごとにスコアを昇順に並べ、それぞれの条件に順位を割り当てます。
| 被験者 | レシピA | レシピB | レシピC |
|---|---|---|---|
| 1 | 2 | 1 | 3 |
| 2 | 2 | 1 | 3 |
| 3 | 2 | 1 | 3 |
| 4 | 2 | 1 | 3 |
| 5 | 1 | 2 | 3 |
| 6 | 2 | 1 | 3 |
| 7 | 2 | 1 | 3 |
| 8 | 2 | 1 | 3 |
| 9 | 1 | 2 | 3 |
| 10 | 2 | 1 | 3 |
順位が同じ場合は平均順位を割り当てます。
② 各条件の順位の平均を計算する
各レシピごとに、割り当てられた順位の平均を計算します。
- レシピAの平均順位 = (2+2+2+2+1+2+2+2+1+2) ÷ 10 = 1.8
- レシピBの平均順位 = (1+1+1+1+2+1+1+1+2+1) ÷ 10 = 1.2
- レシピCの平均順位 = (3+3+3+3+3+3+3+3+3+3) ÷ 10 = 3.0
③ フリードマン統計量を計算する
フリードマン検定の統計量 QQ は以下の式で求めます。
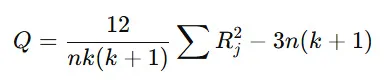
ここで、
- nn = 被験者数(=10)
- kk = 条件数(=3)
- RjR_j = 各条件の順位の合計
順位の合計は次のようになります。
- RA=1.8×10=18R_A = 1.8 \times 10 = 18
- RB=1.2×10=12R_B = 1.2 \times 10 = 12
- RC=3.0×10=30R_C = 3.0 \times 10 = 30
したがって、

この計算により、フリードマン統計量が得られます。
④ 帰無仮説の検定
フリードマン統計量 QQ は、自由度 k−1のカイ二乗分布に従います。ここで、
- k−1=
であるため、カイ二乗分布の臨界値と比較して有意水準5%で帰無仮説を棄却するかを判断します。
2-3 フリードマン検定の結果の解釈
- p値が0.05未満の場合 → 帰無仮説を棄却し、「3つのレシピの評価には統計的に有意な差がある」と判断する。
- p値が0.05以上の場合 → 帰無仮説を棄却できず、「3つのレシピの評価には統計的に有意な差がない」と判断する。
このように、フリードマン検定では順位データを利用して、統計的な有意差を評価できます。
3. Rを使ったフリードマン検定の実装
ここでは、実際にRを用いてフリードマン検定を実行し、その結果を解釈する方法を解説します。統計ソフトRには、フリードマン検定を実施するための関数が用意されており、簡単に計算ができます。本章では、データの準備から検定の実行、結果の解釈、さらに効果量の計算方法までを詳しく説明します。
3-1 Rでのフリードマン検定の実行方法
① データの準備
まず、Rでフリードマン検定を行うために、データを適切な形に整えます。先ほどの食品の評価データをデータフレームとして作成します。
# サンプルデータの作成
data <- data.frame(
被験者 = factor(1:10), # 被験者ID
レシピA = c(7, 6, 8, 5, 9, 6, 7, 5, 8, 6),
レシピB = c(8, 7, 9, 6, 8, 5, 9, 7, 7, 8),
レシピC = c(6, 5, 7, 4, 7, 4, 6, 6, 5, 7)
)
# データの表示
print(data)
このデータフレームには、各被験者が3つのレシピに対して与えた評価スコアが含まれています。
② フリードマン検定の実施
Rでは、friedman.test() 関数を使用することでフリードマン検定を簡単に実行できます。
# フリードマン検定の実行
result <- friedman.test(as.matrix(data[, 2:4]))
# 結果の表示
print(result)
このコードでは、data[, 2:4] の部分で評価スコアのみを抽出し、friedman.test() に渡しています。
3-2 結果の出力と解釈
フリードマン検定の結果は以下のように出力されます。
Friedman rank sum test
data: as.matrix(data[, 2:4])
Friedman chi-squared = 6.8, df = 2, p-value = 0.033
この結果から、
- フリードマン統計量: 6.8
- 自由度 (df): 2
- p値: 0.033
となっています。p値が0.05未満なので、有意水準5%のもとで帰無仮説を棄却し、「3つのレシピには統計的に有意な差がある」と結論づけることができます。
3-3 p値と効果量の計算
フリードマン検定では、p値の他に「効果量」も確認すると、実際にどれほどの差があるのかをより深く理解できます。フリードマン検定の効果量としては、KendallのW(ケンドールの一致係数)が用いられます。これは、0から1の範囲をとり、1に近いほど強い効果があることを示します。
KendallのWを計算する
以下のコードで、KendallのWを計算できます。
# 効果量(KendallのW)の計算
k <- 3 # 条件数
n <- 10 # 被験者数
Q <- result$statistic # フリードマン統計量
W <- Q / (n * (k - 1))
print(W)
この結果が
[1] 0.377
と出た場合、これは中程度の効果があることを示します(KendallのWの基準:0.1=小, 0.3=中, 0.5以上=大)。
4. Q&A(よくある質問)
ここでは、フリードマン検定に関してよく寄せられる質問とその回答をまとめました。
Q1. フリードマン検定と対応のある一元配置分散分析(ANOVA)の違いは?
A. フリードマン検定は非パラメトリック手法であり、データが正規分布していなくても使用できます。一方、対応のある一元配置ANOVA(反復測定ANOVA) は、データが正規分布することを前提としています。そのため、データが正規分布に従っているかどうかを事前に確認し、適切な手法を選択することが重要です。
| 比較項目 | フリードマン検定 | 反復測定ANOVA |
|---|---|---|
| 分析対象 | 対応のあるデータ | 対応のあるデータ |
| 分布の仮定 | 不要 | 必要(正規分布) |
| 変数のタイプ | 順位データでも可 | 連続データが望ましい |
| 外れ値の影響 | 受けにくい | 受けやすい |
| 結果の解釈 | 順位の比較 | 平均値の比較 |
Q2. フリードマン検定の結果が有意だった場合、どの群に違いがあるのかを知るには?
A. フリードマン検定の結果が有意であった場合、どの群間に差があるのかを知るためには、事後検定(多重比較) を実施する必要があります。
代表的な手法としては、
- Nemenyi検定(非パラメトリックの多重比較)
- Wilcoxonの符号付き順位検定(Bonferroni補正付き)
があります。Rでは PMCMRplus パッケージを使ってNemenyi検定を実施できます。
# Nemenyiの事後検定(フリードマン検定後)
install.packages("PMCMRplus")
library(PMCMRplus)
posthoc.friedman.nemenyi.test(as.matrix(data[, 2:4]))
この検定を行うことで、どの条件間に有意な差があるのかを詳しく確認できます。
Q3. フリードマン検定はどんなデータに適用できる?
A. フリードマン検定は、「同じ被験者が複数の条件下で測定されたデータ」 に適用できます。例えば、次のようなデータに適用できます。
✅ 適用可能なデータ
- 医療・心理学:同じ患者に対する3種類の治療法の効果比較
- 食品評価:同じパネリストが異なる食品の味を評価
- マーケティング:同じ顧客が異なる広告デザインを評価
❌ 適用できないデータ
- 対応のない(独立した)グループの比較(→ クラスカル・ウォリス検定を使用)
- 2群のみの比較(→ Wilcoxonの符号付き順位検定を使用)
Q4. サンプルサイズが小さい場合でもフリードマン検定は使える?
A. はい、フリードマン検定は少ないサンプル数(n < 30)でも適用可能 です。ただし、サンプル数が極端に少ない(n < 10)場合、統計的なパワーが低下するため、慎重に解釈する必要があります。
また、小標本の場合はExact Test(厳密検定) を考慮するのも一つの方法です。
5. まとめ
本記事では、フリードマン検定について基礎から応用まで詳しく解説しました。
✅ フリードマン検定のポイント
- 対応のある3群以上のデータを比較する非パラメトリック検定
- データの正規性を仮定しないため、柔軟に適用可能
- 結果が有意なら、事後検定(Nemenyi検定など)で群間の差を確認
- Rを使うと簡単に実施でき、KendallのWで効果量も測定可能
フリードマン検定が適している場面
- 食品の官能評価
- 医療・心理学実験
- マーケティング調査
など、多くの分野で活用できます。
本記事を参考に、ぜひフリードマン検定を活用してデータ分析に役立ててみてください!











