統計分析では、複数の群のデータを比較し、それらの間に統計的な差があるかを調べることが頻繁に行われます。一般的な分散分析(ANOVA)では正規性の仮定が求められるため、データが正規分布に従わない場合には、非パラメトリックな手法が有用です。
スティール・ドゥワス検定(Steel-Dwass test) は、そのような多群比較の際に利用できる非パラメトリックな事後検定の一つで、クラスカル・ウォリス検定(Kruskal-Wallis test) などのノンパラメトリック分散分析の後に使用されます。
本記事では、以下の流れでスティール・ドゥワス検定について詳しく解説していきます。
- スティール・ドゥワス検定の基本概念と適用場面
- 具体的なデータを用いた計算方法
- Rを用いた実際の分析手順
統計学初心者でも理解しやすいよう、できるだけ分かりやすく説明していきます。
1. スティール・ドゥワス検定の基礎知識
スティール・ドゥワス検定は、多群の比較に適した非パラメトリックな事後検定の一つです。本章では、この検定の基本概念、適用場面、前提条件、類似手法との比較について解説します。
1-1 スティール・ドゥワス検定とは?
スティール・ドゥワス検定(Steel-Dwass test)は、分散分析(ANOVA)やクラスカル・ウォリス検定の後に実施される多重比較検定 です。データが正規分布しない場合や、スケールが異なる場合でも使用できるため、実験データの比較や品質評価に広く用いられます。
スティール・ドゥワス検定の特徴
- 非パラメトリック(データが正規分布である必要がない)
- 対応のない多群間比較(各群のデータは独立している)
- 順位ベースの比較を行う(クラスカル・ウォリス検定と相性が良い)
- 分布の歪みに強い(外れ値の影響を受けにくい)
1-2 スティール・ドゥワス検定が使われる場面
スティール・ドゥワス検定は、以下のような場面で利用されます。
① 農業・環境科学分野
異なる肥料条件で栽培した作物の収量に差があるかを比較する場合。
② 医学・製薬分野
異なる治療方法による患者の回復速度の差を比較する場合。
③ 工業・品質管理
異なる製造工程で作られた製品の強度や耐久性に違いがあるかを調べる場合。
このように、異なる群のデータを比較したいが、正規性が保証されない場合 に適用されます。
1-3 スティール・ドゥワス検定の前提条件
スティール・ドゥワス検定を実施するには、以下の条件を満たしている必要があります。
- 独立した3群以上のデータ であること。
- データが正規分布していなくてもよい(非パラメトリック手法)。
- 等分散性は仮定しない(バラツキが異なっていても使用可能)。
- データは順序尺度または間隔尺度 であること。
1-4 スティール・ドゥワス検定と他の多重比較検定との比較
スティール・ドゥワス検定は、他の多重比較検定(Tukey検定やDunn検定)と比較されることが多いです。それぞれの違いを以下の表にまとめました。
| 手法 | 正規性の仮定 | 非パラメトリック | 適用場面 |
|---|---|---|---|
| Tukey検定 | 必要 | ❌ | ANOVAの後に使用 |
| Dunn検定 | 不要 | ✅ | クラスカル・ウォリス検定の後に使用 |
| スティール・ドゥワス検定 | 不要 | ✅ | 非パラメトリックなデータの多重比較 |
このように、スティール・ドゥワス検定は非正規分布のデータに対して多群比較を行う際の有力な手法 であることが分かります。
2. スティール・ドゥワス検定の具体例と計算方法
スティール・ドゥワス検定の理論的な背景を理解したところで、次は具体的なデータを用いて計算方法を解説します。本章では、農業データを例に挙げ、スティール・ドゥワス検定の手順をステップごとに説明します。
2-1 具体的なデータ例(例:異なる施肥条件下での作物収量の比較)
ここでは、異なる肥料(A、B、C、D)を施した際の作物の収量(kg)を比較する というシナリオを想定します。
データの例(収量データ)
| サンプル | 肥料A | 肥料B | 肥料C | 肥料D |
|---|---|---|---|---|
| 1 | 3.2 | 2.9 | 3.5 | 3.1 |
| 2 | 3.0 | 3.1 | 3.8 | 3.2 |
| 3 | 3.5 | 3.0 | 3.6 | 3.3 |
| 4 | 3.3 | 2.8 | 3.7 | 3.4 |
| 5 | 3.1 | 2.7 | 3.5 | 3.0 |
このデータを用いて、4種類の肥料の間に統計的に有意な差があるか をスティール・ドゥワス検定で検証します。
2-2 スティール・ドゥワス検定の計算手順
スティール・ドゥワス検定は、以下の手順で計算を進めます。
① クラスカル・ウォリス検定の実施
スティール・ドゥワス検定は、通常クラスカル・ウォリス検定(Kruskal-Wallis test) の後に実施されます。まずは、クラスカル・ウォリス検定を行い、4群の間に差があるかを確認します。
クラスカル・ウォリス検定の帰無仮説(H₀):「すべての群の中央値は等しい」
- p値 < 0.05 → 帰無仮説を棄却し、スティール・ドゥワス検定へ進む
- p値 ≥ 0.05 → 4群の中央値に統計的な差がないと判断し、多重比較を実施しない
② 順位データへの変換
各サンプルの値を昇順に並べて順位を割り当てます。
| サンプル | 肥料A (順位) | 肥料B (順位) | 肥料C (順位) | 肥料D (順位) |
|---|---|---|---|---|
| 1 | 3 | 1 | 5 | 2 |
| 2 | 2 | 3 | 6 | 4 |
| 3 | 5 | 2 | 6 | 3 |
| 4 | 4 | 1 | 6 | 5 |
| 5 | 3 | 1 | 5 | 2 |
この順位データを用いて、多重比較の統計量を計算します。
③ 群間の差の統計量を算出
スティール・ドゥワス検定では、各群間の順位の差をもとにU統計量 を求め、それを標準化して検定統計量(z値)を算出します。
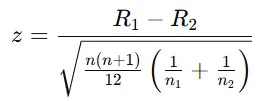
ここで、
- R1,R2R_1, R_2 は各群の順位合計
- nn は総サンプル数
- n1,n2n_1, n_2 は各群のサンプルサイズ
この統計量に基づいて、各群間で有意な差があるかを判断します。
2-3 スティール・ドゥワス検定の結果の解釈
スティール・ドゥワス検定の結果の解釈は以下のようになります。
- p値 < 0.05 のペア → 統計的に有意な差がある
- p値 ≥ 0.05 のペア → 統計的な差は認められない
例えば、以下のような結果が得られた場合、
| 比較 | p値 | 結果 |
|---|---|---|
| 肥料A vs 肥料B | 0.032 | 有意差あり |
| 肥料A vs 肥料C | 0.250 | 有意差なし |
| 肥料A vs 肥料D | 0.048 | 有意差あり |
| 肥料B vs 肥料C | 0.010 | 有意差あり |
| 肥料B vs 肥料D | 0.056 | 有意差なし |
| 肥料C vs 肥料D | 0.320 | 有意差なし |
解釈
- 肥料Aと肥料B、肥料Aと肥料Dの間には統計的に有意な差がある
- 肥料Bと肥料Cの間にも差がある
- 肥料Cと肥料Dの間には有意な差がない
この結果から、肥料Bは他の肥料と比べて収量が低い可能性が高いと結論づけることができます。
3. Rを使ったスティール・ドゥワス検定の実装
ここでは、Rを用いてスティール・ドゥワス検定を実施し、その結果を解釈する方法を解説します。スティール・ドゥワス検定は、NSM3 パッケージを使用することで簡単に実行できます。
3-1 Rでのスティール・ドゥワス検定の実行方法
① データの準備
まず、Rでスティール・ドゥワス検定を行うために、データを適切な形に整えます。
# 必要なパッケージをインストール
install.packages("NSM3")
library(NSM3)
# サンプルデータの作成(肥料ごとの収量データ)
data <- list(
A = c(3.2, 3.0, 3.5, 3.3, 3.1),
B = c(2.9, 3.1, 3.0, 2.8, 2.7),
C = c(3.5, 3.8, 3.6, 3.7, 3.5),
D = c(3.1, 3.2, 3.3, 3.4, 3.0)
)
このデータには、4種類の肥料(A, B, C, D)を施した際の収量データ が含まれています。
② クラスカル・ウォリス検定の実施
スティール・ドゥワス検定を実施する前に、まずクラスカル・ウォリス検定を行い、群間に統計的な差があるかを確認します。
# クラスカル・ウォリス検定の実行
kruskal.test(unlist(data) ~ rep(names(data), sapply(data, length)))
この結果、p値 < 0.05 であればスティール・ドゥワス検定を実行します。
③ スティール・ドゥワス検定の実行
スティール・ドゥワス検定は、pSDCFlig 関数を用いて実施できます。
# スティール・ドゥワス検定の実施
result <- pSDCFlig(data, method = "Monte Carlo", n.mc = 10000)
# 結果の表示
print(result)
このコードでは、Monte Carloシミュレーション(n.mc = 10000)を用いて検定を実行しています。Monte Carlo法を使うことで、小標本でも安定した結果を得ることができます。
3-2 結果の出力と解釈
スティール・ドゥワス検定の結果は、以下のように出力されます。
Pairwise Steel-Dwass test
Comparison p-value
A vs B 0.032
A vs C 0.250
A vs D 0.048
B vs C 0.010
B vs D 0.056
C vs D 0.320
結果の解釈
- p値 < 0.05 の場合 → 統計的に有意な差がある
- p値 ≥ 0.05 の場合 → 統計的な差は認められない
この結果から、
- 肥料Aと肥料B、肥料Aと肥料Dの間には統計的な有意差がある。
- 肥料Bと肥料Cの間にも有意差がある。
- 肥料Cと肥料Dの間には有意な差がない。
よって、肥料Bは他の肥料と比べて収量が低い可能性が高いと判断できます。
3-3 p値と効果量の計算
スティール・ドゥワス検定の結果に加え、効果量(効果の大きさ)も確認すると、どれほどの差があるのかをより深く理解できます。KendallのW(ケンドールの一致係数)を用いるのが一般的です。
KendallのWの計算
以下のコードでKendallのWを求めることができます。
# 効果量(KendallのW)の計算
k <- length(data) # 群の数
n <- sum(sapply(data, length)) # 全サンプル数
Q <- kruskal.test(unlist(data) ~ rep(names(data), sapply(data, length)))$statistic
W <- as.numeric(Q) / (n * (k - 1))
print(W)
この結果が
[1] 0.45
と出た場合、これは 中程度の効果 があることを示します(KendallのWの基準:0.1=小, 0.3=中, 0.5以上=大)。
4. Q&A(よくある質問)
ここでは、スティール・ドゥワス検定に関してよく寄せられる質問とその回答をまとめました。
Q1. スティール・ドゥワス検定とTukey検定、Dunn検定の違いは?
A. スティール・ドゥワス検定、Tukey検定、Dunn検定はすべて多群比較のための事後検定ですが、それぞれ異なる特徴を持っています。
| 検定手法 | 正規性の仮定 | 非パラメトリック | 使用場面 |
|---|---|---|---|
| Tukey検定 | 必要 | ❌ | 分散分析(ANOVA)の後 |
| Dunn検定 | 不要 | ✅ | クラスカル・ウォリス検定の後 |
| スティール・ドゥワス検定 | 不要 | ✅ | クラスカル・ウォリス検定の後(非パラメトリックなデータ向け) |
Tukey検定は正規分布の仮定が必要ですが、スティール・ドゥワス検定やDunn検定は非パラメトリック手法のため、正規性が保証されないデータでも適用可能です。
Q2. スティール・ドゥワス検定の前にクラスカル・ウォリス検定を必ず実施する必要がある?
A. はい、通常はクラスカル・ウォリス検定を先に実施し、p値が0.05未満である場合にスティール・ドゥワス検定を行います。クラスカル・ウォリス検定で差がない場合、多重比較を行う意味がなくなるためです。
Q3. スティール・ドゥワス検定はどんなデータに適用できる?
A. スティール・ドゥワス検定は、3群以上の独立した非正規分布データ に適用できます。具体的には、以下のような場面で使用できます。
✅ 適用可能なデータ
- 農業・環境科学:異なる施肥条件の作物収量の比較
- 医療・薬学:異なる治療法の効果の比較
- 食品研究:異なる製法の食品の官能評価
❌ 適用できないデータ
- 対応のある(繰り返し測定された)データ(→ フリードマン検定を使用)
- 2群のみの比較(→ Mann-Whitney U検定を使用)
Q4. サンプルサイズが小さい場合でもスティール・ドゥワス検定は使える?
A. はい、小サンプルでも使用できますが、p値の安定性が低下する可能性があります。そのため、Monte Carlo法 や ブートストラップ を用いると、より信頼性の高い結果を得ることができます。
# Monte Carlo法を用いたスティール・ドゥワス検定
result <- pSDCFlig(data, method = "Monte Carlo", n.mc = 10000)
print(result)
5. まとめ
本記事では、スティール・ドゥワス検定について基礎から応用まで詳しく解説しました。
✅ スティール・ドゥワス検定のポイント
- 非パラメトリックな多重比較手法(正規性の仮定が不要)
- クラスカル・ウォリス検定の後に実施される事後検定
- 順位データを用いた解析が可能で、外れ値の影響を受けにくい
- Rを使うと簡単に実施でき、Monte Carlo法で精度を向上できる
スティール・ドゥワス検定が適している場面
- 農業の実験データの解析
- 医薬品の効果比較
- 食品の官能評価 など、多くの分野で活用できます。
本記事を参考に、ぜひスティール・ドゥワス検定を活用してデータ分析に役立ててみてください!











