データの可視化には、さまざまなグラフや図表が用いられます。その中でも、棒グラフは最も基本的なグラフのひとつです。棒グラフは、データの値を棒の長さや色などで表現することで、データの傾向をわかりやすく伝えることができます。
棒グラフの色をカスタマイズすることで、データの視認性を向上させ、より効果的にデータの傾向を伝えることができます。例えば、データの傾向を強調するために、特定の棒を別の色で表示したり、グラデーションやパターンを適用したりすることができます。
本記事では、Rで棒グラフの色を自由にカスタマイズする方法について解説します。基本的な方法から応用的な方法まで、さまざまなカスタマイズ方法を紹介するので、ぜひ参考にしてみてください。
例題
4つの異なる製品(A, B, C, D)の売上データを棒グラフで表示する。
データの準備
まず、製品と売上を含むデータフレームを作成します。
# ggplot2 パッケージをロード
library(ggplot2)
# データフレームの作成
data <- data.frame(
Product = c("A", "B", "C", "D"),
Sales = c(200, 150, 300, 250)
)
このスクリプトは以下の各部分から成り立っています:
-
data.frame(): この関数は新しいデータフレームを作成します。データフレームは複数の列を持ち、各列は異なるタイプのデータ(数値、文字列、日付など)を含むことができます。 -
Product = c("A", "B", "C", "D"): この部分では、「Product」という名前の列を作成し、その列に文字列のベクトルc("A", "B", "C", "D")を割り当てています。このベクトルは製品名を表しており、四つの異なる製品(A, B, C, D)を含んでいます。 -
Sales = c(200, 150, 300, 250): こちらは「Sales」という名前の列を作成し、その列に数値のベクトルc(200, 150, 300, 250)を割り当てています。このベクトルは各製品の売上を表しており、それぞれの製品に対する売上額(200, 150, 300, 250)を含んでいます。
結果
このコードを実行すると、以下のようなデータフレームが作成されます:
| Product | Sales |
|---|---|
| A | 200 |
| B | 150 |
| C | 300 |
| D | 250 |
このデータフレームは、製品名とそれに対応する売上額を含んでおり、後続の分析やグラフ作成に使用することができます。たとえば、このデータを使って棒グラフを作成し、各製品の売上を視覚的に比較することができます。
棒グラフの作成
ggplot 関数にデータフレームを渡し、geom_bar 関数で棒グラフを描きます。aes 関数で軸や色を指定します。
# 棒グラフの作成
ggplot(data, aes(x=Product, y=Sales, fill=Product)) +
geom_bar(stat="identity") +
theme_minimal() +
labs(title="Product Sales", x="Product", y="Sales")
-
ggplot(data, aes(x=Product, y=Sales, fill=Product)):ggplot(data, ...):基本的なグラフを作成するためにggplot2パッケージのggplot関数を使用しています。ここでdataは、グラフに使用されるデータフレームです。aes(x=Product, y=Sales, fill=Product):aesはエステティック(見た目)を設定する関数です。x=Productとy=Salesは、それぞれX軸とY軸に表示されるデータを指定しています。fill=Productは、棒グラフの色を製品ごとに異なる色で塗り分けるように指定しています。
-
geom_bar(stat="identity"):geom_barは棒グラフを描画する関数です。stat="identity"オプションは、Y軸の値をデータフレームのSales列から直接取得することを意味します(デフォルトではgeom_barはカウントを使いますが、ここでは具体的な値を表示したいためこのオプションが必要です)。
-
theme_minimal():- グラフの見た目をシンプルにするために
theme_minimalを使用しています。これは、背景やグリッドラインを最小限に抑え、より読みやすいグラフを作成するためのものです。
- グラフの見た目をシンプルにするために
-
labs(title="Product Sales", x="Product", y="Sales"):labs関数を用いて、グラフのタイトルと軸ラベルを設定しています。ここではグラフのタイトルを"Product Sales"とし、X軸に"Product"、Y軸に"Sales"というラベルを付けています。
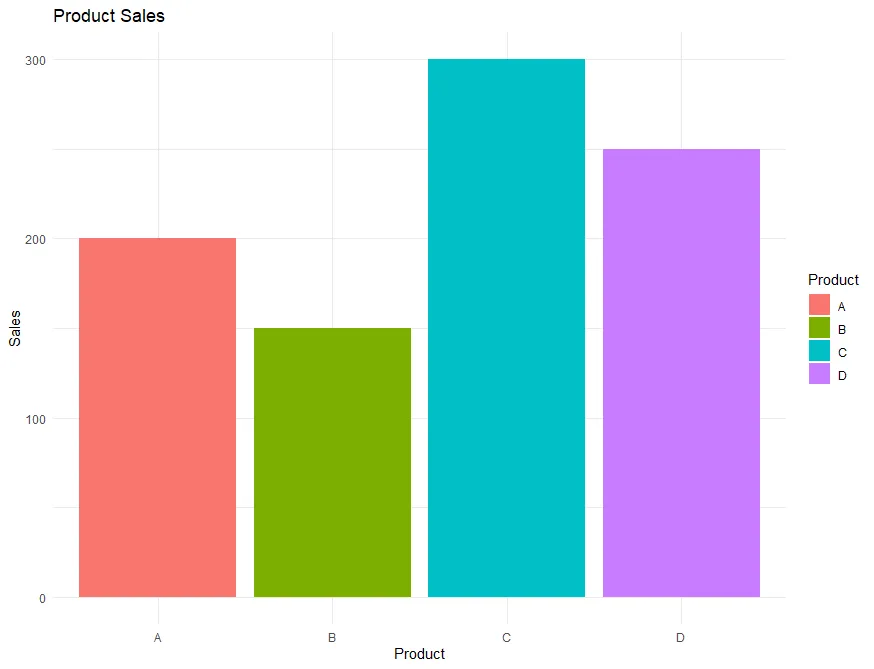
このコードを実行すると、製品ごとの売上を示す色分けされた棒グラフが得られます。製品名がX軸に、それぞれの製品の売上がY軸に表示され、色が製品ごとに異なることで視覚的に区別しやすくなっています。
ここまでのスクリプトを実行すると次のようなグラフになります。
特定の色を指定したい場合
もし特定の色を指定したい場合は、scale_fill_manual 関数を使用して色をカスタマイズできます。
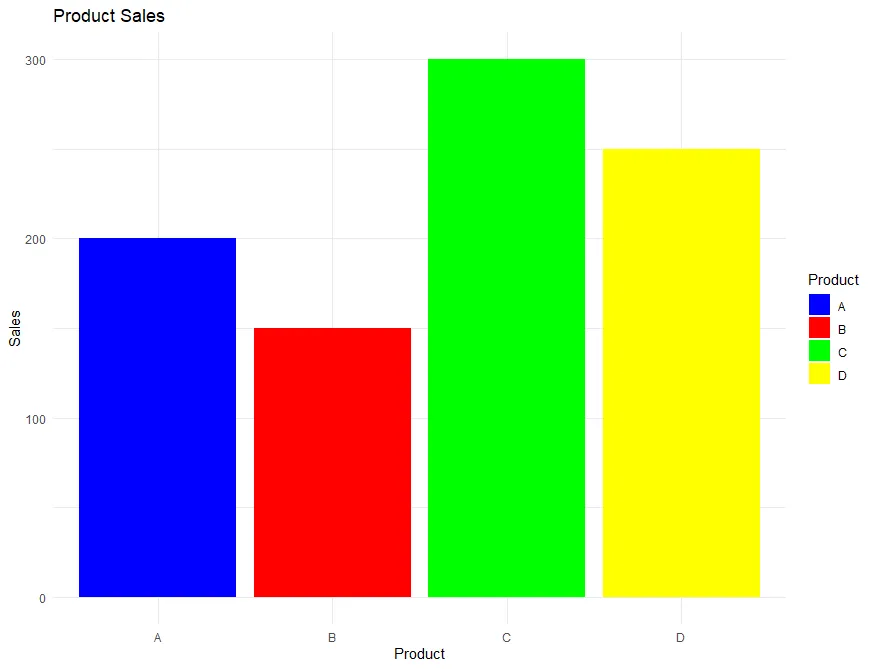
例えば、製品Aを青色、製品Bを赤色、製品Cを緑色、製品Dを黄色で表示したい場合、以下のようにコードを追加します。
ggplot(data, aes(x=Product, y=Sales, fill=Product)) +
geom_bar(stat="identity") +
scale_fill_manual(values=c("A"="blue", "B"="red", "C"="green", "D"="yellow")) +
theme_minimal() +
labs(title="Product Sales", x="Product", y="Sales")
この scale_fill_manual 関数では values 引数に製品名と対応する色の名前(またはHEXコード)を指定しています。これにより、各製品の棒の色が指定した色になります。
このスクリプトを実行すると次のようなグラフになります。
例題2
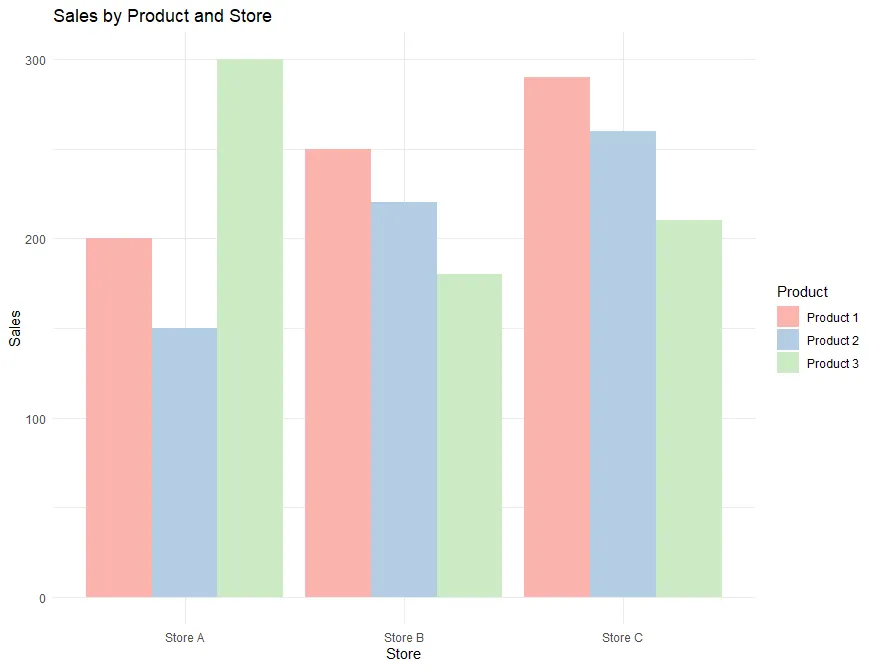
複数の店舗での製品別売上データを色分けした棒グラフで表示するケースを考えてみましょう。
この例では、3つの店舗(Store A, Store B, Store C)と3つの製品(Product 1, Product 2, Product 3)を考慮します。売上データは各店舗での各製品の売上とします。
以下にRスクリプトを示します:
# 必要なライブラリのロード
library(ggplot2)
# データフレームの作成
data <- data.frame(
Store = rep(c("Store A", "Store B", "Store C"), each=3),
Product = rep(c("Product 1", "Product 2", "Product 3"), times=3),
Sales = c(200, 150, 300, 250, 220, 180, 290, 260, 210)
)
# 棒グラフの描画
ggplot(data, aes(x=Store, y=Sales, fill=Product)) +
geom_bar(stat="identity", position=position_dodge()) +
scale_fill_brewer(palette="Pastel1") +
theme_minimal() +
labs(title="Sales by Product and Store", x="Store", y="Sales")データの準備: data.frame 関数を用いて、店舗(Store)、製品(Product)、売上(Sales)の列を持つデータフレームを作成します。rep 関数を使用して、各店舗と製品の組み合わせに対する売上データを割り当てます。
棒グラフの描画: ggplot 関数にデータフレームとエステティック(軸や色の設定)を指定します。geom_bar(stat="identity", position=position_dodge()) で、積み上げではなく並べて表示される棒グラフを描画します。position_dodge() は棒を横に並べるために使用します。
色のカスタマイズ: scale_fill_brewer(palette="Pastel1") を用いて、棒グラフの色をカスタマイズします。ここではPastel1パレットを使用していますが、他のパレットも選択可能です。
グラフの見た目とラベル: theme_minimal() でシンプルなデザインを適用し、labs 関数でグラフのタイトルと軸ラベルを設定します。
このスクリプトを実行すると、店舗ごとに製品別の売上を示す色分けされた棒グラフが生成されます。このグラフでは、各店舗での製品別の売上が一目で比較できるようになっています。
作成されるグラフは次のようになります。