広告 統計検定

無料の統計ソフトRでt検定をやってみよう！初心者向けに分かりやすく解説します

2023年9月18日

統計学は、データの背後にある意味やパターンを明らかにする強力なツールです。

その中でも、ｔ検定は特によく使われる方法の一つです。

この記事では、ｔ検定の基本的な概念と使用方法を初学者向けに解説し、R言語を使ってｔ検定をする方法を解説します。

ｔ検定とは？

ｔ検定は、2つのグループ間の平均の違いを評価する統計的手法です。

例えば、2つの異なる製品の品質、または2つの異なる治療法の効果を比較する際に用いられます。

なぜｔ検定が必要か？

日常生活や研究において、2つのグループ間に違いがあるかどうかを知りたい場面は多々あります。

しかし、単に平均値を比較するだけでは、その違いが偶然に起きたものなのか、実際の違いによるものなのかを区別することはできません。

ｔ検定は、その区別を明確にするツールとして利用されます。

ｔ検定の種類

ｔ検定にはいくつかの種類がありますが、以下の2つが主要なものになりますが、今回は独立2群のt検定のやり方をこの後、解説しています。

  1. 独立2群のt検定：2つの独立したグループ（例：男性と女性の身長）の平均値を比較するためのもの。
  2. 対応のあるt検定：同じグループでの前後の測定データ（例：ダイエット前後の体重）の平均値を比較するためのもの。

ｔ検定の仮説

ｔ検定では、以下の2つの仮説が設定されます。

    • 帰無仮説 ：2つのグループ間には有意な差がない。

    • 対立仮説 ：2つのグループ間には有意な差がある。

ｔ値とは？

ｔ検定の核心となるのは「ｔ値」という統計量です。

ｔ値は、2つのグループの平均値の差をその標準誤差で割ったものです。

このｔ値が大きいほど、2つのグループの平均値には大きな違いがあると判断されます。

ｐ値とは？

ｔ値を元に計算されるのが「p値」という統計量です。p値は、帰無仮説が正しい場合に現在のデータから得られるt値と同等またはそれ以上の極端な、ｔ値が得られる確率を示しています。

p値が特定の閾値（通常は0.05）未満であれば、帰無仮説を棄却し、2つのグループ間に有意な差があると結論します。

注意点と前提条件

ｔ検定を実施する際には、以下の前提条件によって、使う統計手法は別

  • データは正規分布に従っていること。
  • 2つのグループの分散は等しいこと。

これらの前提条件が満たされない場合、他の統計手法を検討する必要があります。
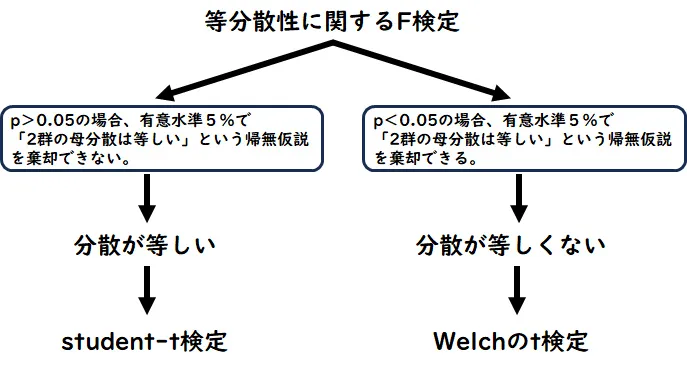
下の例は、正規分布の条件を満たしている場合、等分散かどうかによって手法が異なることを図示したものです。

RでのStuden-t検定のやり方

それでは、R言語を使ってt検定を行う手順を説明します。
まず、以下のようなcsvファイルデータを用意します。ファイル名は「score.csv」になります。

Rではエクセルファイルを読み込むことも出来なくはないのですがちょっとだけ手間がかかります。
csvファイルであればR言語でもそのまま読めるのでここでは、以下の内容のcsvファイルデータを起点に説明を始めます。

「control」群には10個の数値、「drug」群にも10個の数値があるデータを例に解析を行います。

それでは、Ｒでこの「score.csv」ファイルを読み込んでいきます。
以下のように、左上のSourceペインに入力します。

df <- read.csv("D:/ブログ用/17R/R#3 student t/score.csv")

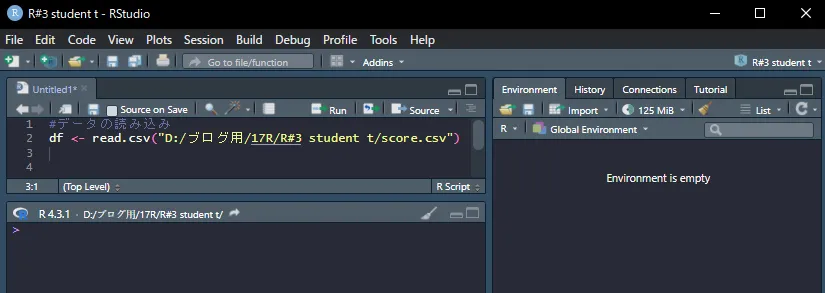
「＃」に続けて「データの読み込み」と書いてあります。
「＃」にはメモ機能があり、#の後の文字列はRの計算には反映されません。
Rコマンドの意味を後から確認したい場合に便利な機能です。

csvファイルを読み込むには、read.csv(”ファイルの場所/ファイル名”)、と記述します。

今回は上の写真のフォルダにscore.csvファイルを保存してありますので、ファイルの場所は
「D:/ブログ用/17R/R#3 student t/score.csv」
となります。

みなさんのファイルがどこに保存されているかによって、この部分の表記は変える必要があります。

次に、2行目を選択して、「Ctrl」キーと「Enter」キーを押してコマンドを実行してください。

すると、dfという変数にscore.csvファイルの内容が代入されます。

すると、右上のEnviromnentペインにdfが登場します。

Environmentペイン内のdfをクリックすると、左上のSourceペインにdfの内容が出てきます。

sorce.csvファイルの内容と同じものが出てきています。
これで、csvファイルがＲに正しく読み込めていることが確認出来ます。
次に以下のコマンドを追記してください。

t_result <- t.test(df$control, df$drug,var.equal=TRUE)
print(t_result)

student-tテストの、コマンドは「t.test(群１,群２,var.equal=TRUE)」を使います。

"var.equal"はR の t.test 関数において、2つの独立した群の分散が等しいか等しくないかを指定するための引数です。

具体的には、var.equal の設定は以下のようになります。

var.equal = TRUE :
2つの群の分散が等しいと仮定して、等分散のt検定（Studentのt検定）を実行します。

var.equal = FALSE
:2つの群の分散が等しくないと仮定して、異分散のt検定（Welchのt検定）を実行します。

df$controlの意味は、dfのcontrolの列（群）を指定するということです。同様にdf$drugは、dfのdrugの列（群）を指定することを意味します。print(t_result)は、t_resultを表示(print)するという意味になります。それでは、実行してください。

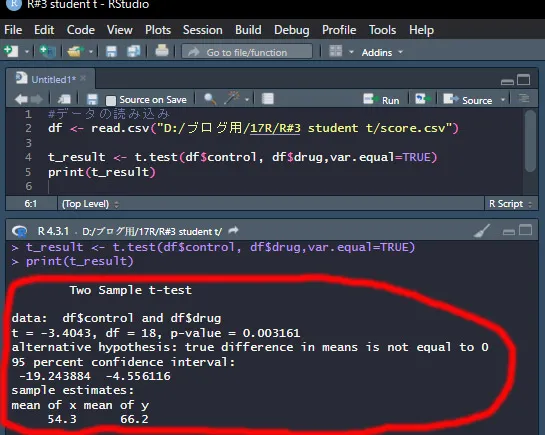
すると、左下に結果が表示されました。
p-value=0.003161となっていて、p<0.05なので、「2つのグループ間で有意な差はない」という帰無仮説が棄却されます。つまり、２つのグループには有意な差があるということになります。

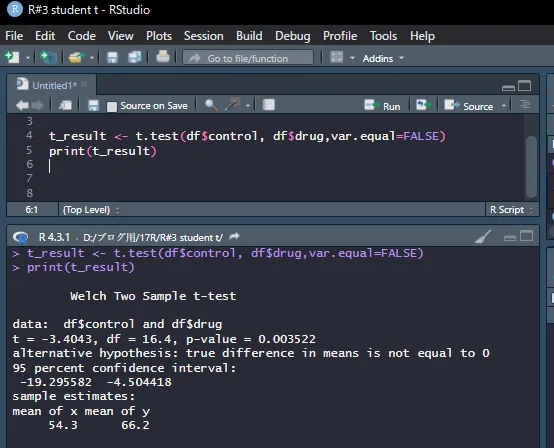
Welchのt検定を行う場合は、var.equal=TRUEをvar.equal=FALSEに変えて実行します。

Welchのt検定の結果はこのようになります。

student-tよりWelchのt検定の方が、理屈からいって有意差が出にくいです。
ｐ値もstudentで「0.003161」であった値が、「0.003522」に大きくなっていることからも分かります。

異分散のt検定（Welchのt検定）は、分散が等しい場合でも等しくない場合でも適切に動作するとされるため、分散の等質性に不安がある場合は var.equal = FALSE をデフォルトとして選択するのも一つの方法です。

ちなみに、私はいつもWelchを選んでいます。F検定するのが面倒なので・・・

順番が前後してしまったのですが、最後にＦ検定のやり方を説明したいと思います。

Ｆ検定のやり方

F検定には、var.test(群１,群２)を使います。

csvファイルを読み込むところからスクリプトを記載します。

＃データの読み込み
df ＜- read.csv("D:/ブログ用/17R/R#3 student t/score.csv")
＃F検定
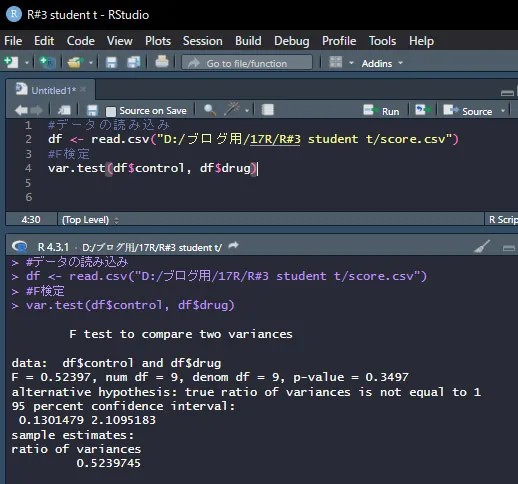
var.test(df$control, df$drug)

p値が0.3497でありp>0.05なので、有意水準5％で「2群の母分散は等しい」という帰無仮説を棄却（否定）できないという結果です。

「2群の母分散は等しい」を否定できないということは、裏を返せば「2群の母分散は等しい」ということですね。

よって、このデータでは等分散を仮定したStudent-t検定をやってもいいよということになります。

以上で、今回の記事は終了です。
最後まで読んでいただきありがとうございました。

統計検定

2025/2/26

スティール・ドゥワス検定とは？多群比較に適した非パラメトリック手法を徹底解説！

統計分析では、複数の群のデータを比較し、それらの間に統計的な差があるかを調べることが頻繁に行われます。一般的な分散分析（ANOVA）では正規性の仮定が求められるため、データが正規分布に従わない場合には、非パラメトリックな手法が有用です。 スティール・ドゥワス検定（Steel-Dwass test） は、そのような多群比較の際に利用できる非パラメトリックな事後検定の一つで、クラスカル・ウォリス検定（Kruskal-Wallis test） などのノンパラメトリック分散分析の後に使用されます。 本記事では、以 ...

ReadMore

統計検定

2025/2/26

フリードマン検定とは？分かりやすく解説！原理・具体例・Rでの実装まで徹底解説

統計学において、データの比較を行う手法は数多く存在します。その中でも、「フリードマン検定」は、対応のある3群以上のデータを比較するための非パラメトリックな方法です。本記事では、フリードマン検定の基本概念から具体例、Rを使った実装までを詳しく解説します。 フリードマン検定は、対応のあるデータに適用されるため、たとえば同じ被験者に対して異なる条件下でのテストを行う場合に有効です。例えば、ある食品メーカーが新しい3種類のレシピを開発し、同じパネリストに試食してもらった場合、それぞれの食品の評価に違いがあるかをフ ...

ReadMore

統計検定

2024/2/28

クラスカルウォリス検定とは？　実際にRでやってみよう

統計学の中でも特に興味深いツールであるクラスカル・ウォリス検定について、より深く掘り下げてみましょう。この検定は、特にサンプルサイズが小さい場合や、データが正規分布に従わない場合に重宝されます。 クラスカル・ウォリス検定とは何か？ クラスカル・ウォリス検定（Kruskal-Wallis test）は、簡単に言うと、3つ以上のグループのデータが同じ特性を持っているかどうか（言い換えると、サンプル群の中央値に差があるかどうか）を調べるための統計的手法です。これは、通常の分散分析（ANOVA）の代わりに使われる ...

ReadMore

特殊なグラフ

2024/4/26

R言語でQQプロットを作成する方法

はじめに QQプロット（Quantile-Quantileプロット）は統計分析で非常に役立つツールです。これを使って、データセットが特定の理論分布に従っているかどうかを視覚的に評価することができます。R言語には、この種のプロットを簡単に作成できる強力なツールが用意されています。この記事では、R言語を使用してQQプロットを作成する基本的なステップを説明します。 必要なパッケージ QQプロットを描くためには、基本的にstatsパッケージが必要ですが、これはRの標準パッケージに含まれているため、特別なインストー ...

ReadMore

グラフのカスタマイズ

2024/4/17

Rでエラーバー付きのグラフを作成する方法

はじめに データの可視化において、エラーバーはデータの変動や不確実性を表現する重要な手段です。R言語を用いたグラフ作成においてエラーバーを追加する方法を学ぶことで、データの解釈をより深く行うことが可能になります。この記事では、基本的なエラーバーの追加方法から、カスタマイズする方法までを段階的に解説します。 エラーバーを含むグラフの重要性 エラーバーは、データ点のばらつきや測定の不確かさを表すのに役立ちます。科学研究や技術報告でよく見られるこの表現方法は、データの信頼性や有効性を視覚的に伝えるために不可欠で ...

ReadMore

グラフのカスタマイズ

2024/4/17

R言語でのグラフ作成：X軸とY軸のスケール比の設定方法

はじめに R言語はデータ分析と可視化に非常に強力なツールです。特にグラフ作成機能は多くのデータサイエンティストや研究者に利用されています。この記事では、R言語でグラフを作成する際にX軸とY軸のスケール比を設定する方法を詳しく解説します。スケール比を調整することで、データの比率や関係性をより正確に表現することが可能になります。 グラフの基本的な作成方法 まず、R言語で基本的なグラフを作成する方法から見ていきましょう。ここでは、plot() 関数を使用してシンプルな散布図を描きます。 # サンプルデータの生成 ...

ReadMore

統計学基礎

2025/2/27

多重共線性とは？統計分析への影響と対策、Rでの検出方法を徹底解説！

統計分析や機械学習において、説明変数（独立変数）同士が強い相関を持つこと は、回帰モデルの推定精度を低下させる可能性があります。 このような状況を 「多重共線性（Multicollinearity）」 と呼びます。 多重共線性が起こると何が問題か？ ✅ 回帰係数の推定値が不安定 になり、解釈が難しくなる✅ 統計的な有意性（p値）が正しく評価できなくなる✅ モデルの予測精度が低下 し、新しいデータに対して適用しにくくなる 例えば、以下のようなデータセットを考えます。 ...

ReadMore

統計学基礎

2025/2/26

ベイズ統計学とは？事前確率と事後確率を用いた推論の基礎からRでの実装まで徹底解説！

統計学において、「新しい情報を得たときに、既存の知識をどのように更新するか？」という問題は非常に重要です。その問題に答えるのがベイズ統計学 です。 ベイズ統計学（Bayesian Statistics） は、事前確率（prior probability）と新しいデータの尤度（likelihood）を組み合わせ、事後確率（posterior probability）を求めることで推論を行います。 例えば、以下のようなケースで活用されています。 ✅ 医療診断：「ある検査で陽性が出た場合、本当に病 ...

ReadMore

統計学基礎

2025/2/27

時系列解析の基礎と応用｜データの変動パターンを理解し予測に活かす方法

時系列データは、時間の経過とともに変化するデータのことであり、売上・株価・気象データ・センサーデータ など、さまざまな分野で活用されています。 時系列解析とは？時系列解析は、データの傾向やパターンを分析し、将来の予測や異常検知を行うための手法 です。 ✅ 時系列解析の主な目的 過去のデータをもとに将来を予測する（売上予測・需要予測） 季節性やトレンドを把握する（消費行動のパターン分析） 異常値を検出し、異常なイベントを特定する（センサーデータの監視） 例えば、以下のようなデータを時系列解析で ...

ReadMore

-統計検定
-

S