広告 統計検定

ウィルコクソンの符号付順位和検定（Wilcoxon Signed-Rank Test）とは？ 実際にRでやってみよう

2023年11月17日

ウィルコクソンの符号付順位和検定（Wilcoxon Signed-Rank Test）は、統計学において広く使われているノンパラメトリックな検定方法です。この検定は、特にサンプルサイズが小さい場合やデータが正規分布に従わない場合に有効で、対応する2つのサンプル間の中央値の差異が偶然によるものかどうかを評価するために使用されます。以下では、この検定の基本的な概念、手順、適用例、注意点を初学者向けに詳しく解説します。

ウィルコクソンの符号付順位和検定の基本概念とは

ウィルコクソンの符号付順位和検定は、2つの関連するサンプル（例えば、同じ個体に対する前後の測定値）間の中央値の差が統計的に有意かどうかを調べるための方法です。この検定は、データが正規分布に従っていない場合や、サンプルサイズが小さい場合に特に有用です。正規分布に従わないデータの場合、従来のt検定よりもこの検定の方が適切な結果をもたらすことがあります。

ウィルコクソンの符号付順位和検定のやり方（手順）

ウィルコクソン検定を行う際の主な手順は以下の通りです。

  1. 差の計算: まず、2つのサンプル間の差を計算します。例えば、ある治療法を施した前後の患者の症状の改善度を測定したとします。ここでは、それぞれの患者の治療前後の症状の改善度を比較し、その差を求めます。

  2. 順位の付与: 次に、これらの差の絶対値に順位を付けます。差の大きさが同じ場合は、その順位の平均値を割り当てます。

  3. 符号の付与と和の計算: 差の符号（正か負か）を順位に適用します。そして、正の差の順位和と負の差の順位和をそれぞれ計算します。

  4. 統計量の決定: 一般に、より小さい方の順位和を検定統計量として使用します。この値は、後で分布表と比較してP値を求めるために用います。

  5. 結果の解釈: 計算された統計量をウィルコクソンの分布と比較し、P値を求めます。このP値に基づいて、2つのサンプル間に統計的に有意な差があるかどうかを判断します。

ウィルコクソンの符号付順位和検定の注意点とは

この検定は、サンプルサイズが非常に小さい場合や、データが正規分布に従う場合には注意が必要でその場合はパラメトリックな検定方法（例えば、対応のあるt検定）を使ってください。
サンプルサイズが小さい場合、結果の解釈には慎重である必要があります。

サンプルサイズが小さいときの問題点

  1. 統計的検出力が低い: サンプルサイズが小さいと、検定が実際に存在する効果（例えば、治療の効果）を検出する能力（検出力）が低くなります。つまり、本当に差が存在しても、それを統計的に「有意」として検出できない可能性が高くなります。

  2. 結果の一般化の問題: 小さいサンプルサイズで得られた結果は、より大きな母集団に対して一般化することが難しくなります。サンプルが母集団を代表していない可能性があるため、結果が特定のサンプルに特有のものである可能性があります。

  3. ランダム変動の影響が大きい: 小さいサンプルでは、ランダムな変動が結果に大きく影響する可能性があります。これは、少数の異常値が全体の結果に大きく影響を与えることを意味します。

慎重な解釈のためのアプローチ

  1. 結果の限定的な解釈: 小さいサンプルで得られた結果は、あくまで探索的なものとして解釈することが重要です。結果を「確固たる証拠」として捉えるのではなく、仮説生成の一環として考えるべきです。

  2. 追加研究の必要性の強調: 初期の結果をもとに、より大きなサンプルサイズを持つ研究を行う必要があることを明確にします。これにより、初期の結果が偶然でないことを確かめることができます。

  3. 信頼区間の使用: 結果の報告時には、P値だけでなく信頼区間も併せて報告することが有効です。信頼区間は結果の不確実性を示すため、その幅が広い場合は結果に対する自信が低いことを示します。

  4. 文脈や既存の知識との比較: 結果を関連する他の研究や理論的な枠組みと比較することで、その妥当性を評価します。既存の知識と一致する、あるいはそれに反する結果であれば、その意味するところを慎重に考察する必要があります。

ここまでのまとめ

ウィルコクソンの符号付順位和検定は、非常に汎用性が高く、特に小規模な研究や正規分布を仮定できないデータにおいて有効な統計的ツールです。この検定を適切に理解し、使用することで、データからの深い洞察を得ることが可能になります。

例題を手計算してみよう！

例題

あるサプリメントが睡眠の質に与える影響を調べるために、10人の被験者にサプリメントを摂取させ、摂取前後で睡眠の質を点数化して比較します。睡眠の質は数値で評価し、高いほど良い睡眠を表します。睡眠の質に変化があるかどうか有意水準0.05で検定しなさい。

対象者12345678910
摂取前の睡眠の質
(before)		80776856656666678866
摂取後の睡眠の質
(after)		80869067806081739574

解答

帰無仮説：サプリメントの摂取によって睡眠の質に変化は無い
対立仮説：サプリメントの摂取によって睡眠の質に変化がある

まず、次の表のとおり｜前ー後｜と順位を求めます。
すると次のようになります。

対象者12345678910
前ー後0-9-22-11-156-15-6-7-8
｜前ー後｜09221115615678
順位-5967.51.57.51.534

順位は｜前ー後｜の値の小さい方から付けます。
同順位は平均順位とします。また、差がゼロのものは順位付けしません。

次に順位の和を計算します。

前＞後の組の順位の和＝1.5
後＞前の組の順位の和＝5+9+6+7.5+7.5+1.5+3+4＝43.5

上の結果より検定統計量T=1.5

α＝0.05で、n=9(前＝後の場合が１つあったので10-1=9)の棄却限界値は次の表より、5となります。

T＝1.5＜5　この検定では帰無仮説を棄却します。
ウィルコクソンの符号付順位和検定では、値の小さい方を検定統計量とし、先ほどの棄却限界値の表がnの増加と共に増加しているので、帰無仮説はｚ分布やt分布などとは逆に、検定統計量≦棄却限界値の時に棄却されるからです。

結論
有意水準５％で、サプリメントの摂取が睡眠の質に有意な影響を与えたと考えることができます。

例題を無料の統計ソフトR言語で検定しよう！

R言語のスクリプトは

先ほど手計算した例題をR言語で検定してみましょう。
RとR-Studioのインストール方法など基本的な操作については過去の記事を参考にしてください。

スクリプトは次のようになります。

# サンプルデータの設定
before <- c(80, 77, 68, 56, 65, 65, 66, 67, 88, 66)
after  <- c(80, 86, 90, 67, 80, 60, 81, 73, 95, 74)

# ウィルコクソンの符号付順位和検定の実行
test_result <- wilcox.test(after, before, paired = TRUE)

# 結果の表示
print(test_result)

すると結果は次のようになります。

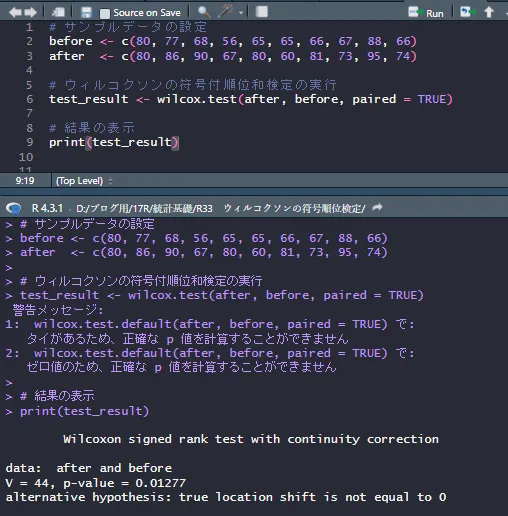
ウィルコクソンの符号付順位和検定を行った際に表示される「タイがあるため、正確な p 値を計算することができません」という警告メッセージについて説明します。

警告メッセージの意味

この警告は、データセット内に「タイ」（同じ値を持つデータ点）が存在することを意味します。ウィルコクソン検定では、データ点に順位を付ける際に、同じ値を持つデータ点があると、それらに対して正確な順位を割り当てることが難しくなります。このため、計算された p 値は「近似値」として扱われ、統計的な解釈においては慎重である必要があります。

解釈の方法

  1. 近似的な p 値: 警告メッセージは、計算された p 値が完全に正確ではないことを示しています。ただし、この p 値はまだ有用な情報を提供し、データセットの傾向を理解するための参考になります。

  2. データの確認: タイが多い場合は、データセットをより詳細に検討し、その特性を理解することが重要です。例えば、測定の精度や方法に問題がないかを再評価することが考えられます。

  3. 他の方法の検討: タイが多い場合、他の統計的手法を検討する価値があります。例えば、非パラメトリックな別の検定方法（例えばマクマネー検定など）を試してみるなど。

正確性について

警告メッセージが示す「正確でない」という程度は、一概に定量化することは難しいです。しかし、通常、タイの数が多くなるほど、p 値の不確実性は大きくなります。このため、結果の解釈には慎重さが求められますが、それでも検定結果は有意な洞察を提供することが多いです。

この警告メッセージは、データの特性や検定の限界を理解するための重要な手がかりとなります。データ解析においては、このような警告を適切に解釈し、必要に応じて他のアプローチを検討することが重要です。

検定結果

  1. 検定の結果として得られたP値を確認すると、ｐ＝0.01277です。通常、統計学ではP値が0.05以下であれば、結果を統計的に有意とみなします。つまり、P値が0.05以下であれば、サプリメントの摂取が睡眠の質に有意な影響を与えたと考えることができます。先ほどの手計算と同じ結果ですね。

  2. 警告メッセージの考慮: もし結果に警告メッセージがあった場合（例えば、タイに関する警告）、その影響を考慮に入れます。子の例題でも警告文が出ております。タイが多い場合、P値は近似値として解釈し、結果には慎重な態度を取る必要があります。

  3. 実質的な意味: 統計的に有意な結果が得られたとしても、それが実際にどの程度の効果を持つかは別の問題です。例えば、睡眠の質の向上が統計的には有意でも、その改善の大きさ（効果量）が実用的に十分かどうかを考慮する必要があります。

  4. データの特性の再検討: 任意の統計的検定の結果を解釈する際には、使用したデータの特性（分布の形状、外れ値の存在など）を再検討し、それらが結果にどのような影響を与えているかを考慮することが重要です。

結果の解釈には、得られた統計的な数値だけでなく、データの質、研究デザイン、実験の文脈など、多角的な観点からの考慮が必要です。また、統計的に有意な結果が得られたとしても、それが必ずしも実際の効果を意味するわけではないことを理解しておくことも大切です。

特殊なグラフ

2024/4/26

R言語でQQプロットを作成する方法

はじめに QQプロット（Quantile-Quantileプロット）は統計分析で非常に役立つツールです。これを使って、データセットが特定の理論分布に従っているかどうかを視覚的に評価することができます。R言語には、この種のプロットを簡単に作成できる強力なツールが用意されています。この記事では、R言語を使用してQQプロットを作成する基本的なステップを説明します。 必要なパッケージ QQプロットを描くためには、基本的にstatsパッケージが必要ですが、これはRの標準パッケージに含まれているため、特別なインストー ...

ReadMore

グラフのカスタマイズ

2024/4/17

Rでエラーバー付きのグラフを作成する方法

はじめに データの可視化において、エラーバーはデータの変動や不確実性を表現する重要な手段です。R言語を用いたグラフ作成においてエラーバーを追加する方法を学ぶことで、データの解釈をより深く行うことが可能になります。この記事では、基本的なエラーバーの追加方法から、カスタマイズする方法までを段階的に解説します。 エラーバーを含むグラフの重要性 エラーバーは、データ点のばらつきや測定の不確かさを表すのに役立ちます。科学研究や技術報告でよく見られるこの表現方法は、データの信頼性や有効性を視覚的に伝えるために不可欠で ...

ReadMore

グラフのカスタマイズ

2024/4/17

R言語でのグラフ作成：X軸とY軸のスケール比の設定方法

はじめに R言語はデータ分析と可視化に非常に強力なツールです。特にグラフ作成機能は多くのデータサイエンティストや研究者に利用されています。この記事では、R言語でグラフを作成する際にX軸とY軸のスケール比を設定する方法を詳しく解説します。スケール比を調整することで、データの比率や関係性をより正確に表現することが可能になります。 グラフの基本的な作成方法 まず、R言語で基本的なグラフを作成する方法から見ていきましょう。ここでは、plot() 関数を使用してシンプルな散布図を描きます。 # サンプルデータの生成 ...

ReadMore

統計検定

2025/2/26

スティール・ドゥワス検定とは？多群比較に適した非パラメトリック手法を徹底解説！

統計分析では、複数の群のデータを比較し、それらの間に統計的な差があるかを調べることが頻繁に行われます。一般的な分散分析（ANOVA）では正規性の仮定が求められるため、データが正規分布に従わない場合には、非パラメトリックな手法が有用です。 スティール・ドゥワス検定（Steel-Dwass test） は、そのような多群比較の際に利用できる非パラメトリックな事後検定の一つで、クラスカル・ウォリス検定（Kruskal-Wallis test） などのノンパラメトリック分散分析の後に使用されます。 本記事では、以 ...

ReadMore

統計検定

2025/2/26

フリードマン検定とは？分かりやすく解説！原理・具体例・Rでの実装まで徹底解説

統計学において、データの比較を行う手法は数多く存在します。その中でも、「フリードマン検定」は、対応のある3群以上のデータを比較するための非パラメトリックな方法です。本記事では、フリードマン検定の基本概念から具体例、Rを使った実装までを詳しく解説します。 フリードマン検定は、対応のあるデータに適用されるため、たとえば同じ被験者に対して異なる条件下でのテストを行う場合に有効です。例えば、ある食品メーカーが新しい3種類のレシピを開発し、同じパネリストに試食してもらった場合、それぞれの食品の評価に違いがあるかをフ ...

ReadMore

統計検定

2024/2/28

クラスカルウォリス検定とは？　実際にRでやってみよう

統計学の中でも特に興味深いツールであるクラスカル・ウォリス検定について、より深く掘り下げてみましょう。この検定は、特にサンプルサイズが小さい場合や、データが正規分布に従わない場合に重宝されます。 クラスカル・ウォリス検定とは何か？ クラスカル・ウォリス検定（Kruskal-Wallis test）は、簡単に言うと、3つ以上のグループのデータが同じ特性を持っているかどうか（言い換えると、サンプル群の中央値に差があるかどうか）を調べるための統計的手法です。これは、通常の分散分析（ANOVA）の代わりに使われる ...

ReadMore

-統計検定
-

S