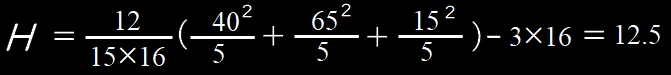統計学の中でも特に興味深いツールであるクラスカル・ウォリス検定について、より深く掘り下げてみましょう。この検定は、特にサンプルサイズが小さい場合や、データが正規分布に従わない場合に重宝されます。
クラスカル・ウォリス検定とは何か?
クラスカル・ウォリス検定(Kruskal-Wallis test)は、簡単に言うと、3つ以上のグループのデータが同じ特性を持っているかどうか(言い換えると、サンプル群の中央値に差があるかどうか)を調べるための統計的手法です。これは、通常の分散分析(ANOVA)の代わりに使われることが多く、特にデータが特定のパターン(正規分布)に従わない時や、データの量が少ない時に役立ちます。
クラスカル・ウォリスの手順
手順① 順位付け
この検定では、全てのデータポイントを一つにまとめて、最小値から順に順位付けします。この順位付けにおいて、同じ値を持つデータ点がある場合は、それらに平均順位を割り当てます。順位付けは、個々のデータ値の代わりに、その相対的な位置を用いるため、異なるグループ間でのデータの分布の違いをより適切に捉えることができます。
手順② 検定統計量 H の計算
ここでの重要なステップは、各グループのランク和を用いて検定統計量Hを計算することです。この
H 統計量は、グループ間でデータの分布がどの程度異なるかを示す指標となります。この計算により、グループ間でのデータのバリエーションを数値化することができます。
H統計量は次の式になります。
ここで、
Rj:j群の順位の和
nj:j群のデータ数
n:すべてのデータ数
Hは自由度 f=k-1のカイ二乗分布に従います。
手順③ p値の計算と結論の導出
次に、計算された H 統計量に基づいて、p値を決定します。このp値は、観測されたデータがグループ間で有意な差がないという帰無仮説の下で生じる確率を示します。p値が事前に設定された有意水準(通常は0.05)よりも小さい場合、我々は帰無仮説を棄却し、グループ間に統計的に有意な差が存在すると結論付けます。
まとめ
クラスカル・ウォリス検定は、データの分布が正規でない場合やサンプルサイズが小さい場合に特に有用です。しかし、この検定はどのグループが異なるのかを特定することはできません。したがって、有意な結果が出た場合は、どのグループが異なるかを明らかにするための追加のポストホック検定が必要となります。この検定をマスターすることで、より深いデータ分析が可能になり、統計学の理解が一層深まります。
例題を解いてみましょう
例題:ダイエットプログラムの効果比較
3つの異なるダイエット方法A、B、Cの効果を比較する研究を考えます。
ある研究で、3種類のダイエットプログラム(A、B、C)の効果を比較しています。
各プログラムは異なるグループの参加者に適用され、6週間後の体重減少量(kg)が記録されました。
参加者とデータ
-
プログラムA: 5人の参加者
体重減少量: 2.0, 2.1, 1.9, 2.2, 2.3 kg
-
プログラムB: 5人の参加者
体重減少量: 3.1, 3.6, 3.4, 3.0, 3.2 kg
-
プログラムC: 5人の参加者
体重減少量: 1.5, 1.4, 1.6, 1.8, 1.7 kg
クラスカル・ウォリス検定の実施
手順① 順位付け
効果の低い最小のものから順に順位付けしていきます。
順位付けすると、次の表のようになります。
| 1人目 | 2人目 | 3人目 | 4人目 | 5人目 |
| プログラムA | 7 | 8 | 6 | 9 | 10 |
| プログラムB | 12 | 15 | 14 | 11 | 13 |
| プログラムC | 2 | 1 | 3 | 5 | 4 |
手順② 検定統計量Hの計算
RA=7+8+6+9+10=40
RB=12+15+14+11+13=65
RC=2+1+3+5+4=15
よって、Hは次のようになります
手順③ 結論の導出(p値はRを使って後ほど計算します)
p値を出すにはRを使ってあとで算出します。
ここでは表を使った方法で解いていきます。
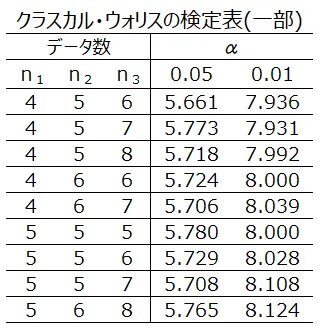
α=0.05で3群がそれぞれ5の時の棄却限界値は次の表より、5.78になります
H=12.5>5.78なので、帰無仮説(3つの群の母代表値に差は無い)を棄却します。
したがって、結論は3つのダイエットプログラム(A、B、C)間で体重減少量には統計的に有意な違いがあると結論づけることができます。
Rを使ってクラスカルウォリス検定をやろう!
先ほどの例題をRを使って検定してみましょう。
スクリプトは次のとおりです。
# データの準備
data_A <- c(2.0, 2.1, 1.9, 2.2, 2.3)
data_B <- c(3.1, 3.6, 3.4, 3.0, 3.2)
data_C <- c(1.5, 1.4, 1.6, 1.8, 1.7)
# 全データを統合し、グループのラベルを付ける
data <- c(data_A, data_B, data_C)
group <- factor(c(rep("A", length(data_A)), rep("B", length(data_B)), rep("C", length(data_C))))
# クラスカル・ウォリス検定の実行
kruskal.test(data ~ group)
# 結果は自動的に表示されます
Rスクリプトを実行すると次のような結果になります。
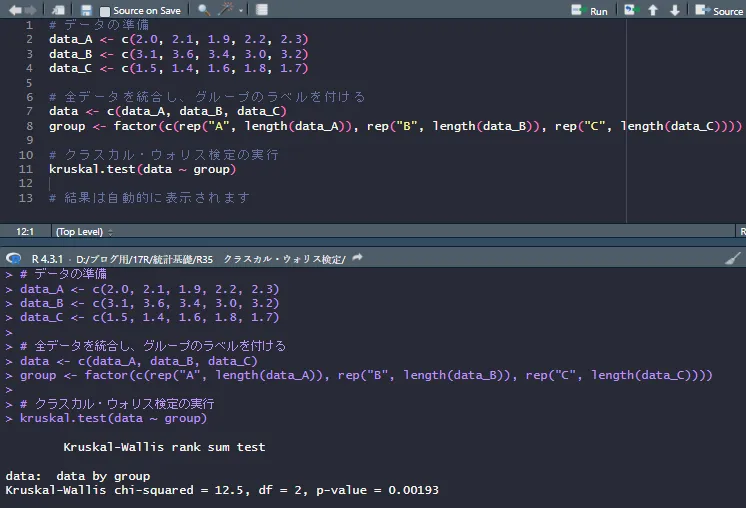
H=12.5、p値=0.00193<0.05という結果になりましたので、有意差ありという結果です。
先ほどの手計算の結果と同じですね。

統計検定
2025/2/26
スティール・ドゥワス検定とは?多群比較に適した非パラメトリック手法を徹底解説!
統計分析では、複数の群のデータを比較し、それらの間に統計的な差があるかを調べることが頻繁に行われます。一般的な分散分析(ANOVA)では正規性の仮定が求められるため、データが正規分布に従わない場合には、非パラメトリックな手法が有用です。 スティール・ドゥワス検定(Steel-Dwass test) は、そのような多群比較の際に利用できる非パラメトリックな事後検定の一つで、クラスカル・ウォリス検定(Kruskal-Wallis test) などのノンパラメトリック分散分析の後に使用されます。 本記事では、以 ...
ReadMore

統計検定
2025/2/26
フリードマン検定とは?分かりやすく解説!原理・具体例・Rでの実装まで徹底解説
統計学において、データの比較を行う手法は数多く存在します。その中でも、「フリードマン検定」は、対応のある3群以上のデータを比較するための非パラメトリックな方法です。本記事では、フリードマン検定の基本概念から具体例、Rを使った実装までを詳しく解説します。 フリードマン検定は、対応のあるデータに適用されるため、たとえば同じ被験者に対して異なる条件下でのテストを行う場合に有効です。例えば、ある食品メーカーが新しい3種類のレシピを開発し、同じパネリストに試食してもらった場合、それぞれの食品の評価に違いがあるかをフ ...
ReadMore

統計検定
2024/2/28
クラスカルウォリス検定とは? 実際にRでやってみよう
統計学の中でも特に興味深いツールであるクラスカル・ウォリス検定について、より深く掘り下げてみましょう。この検定は、特にサンプルサイズが小さい場合や、データが正規分布に従わない場合に重宝されます。 クラスカル・ウォリス検定とは何か? クラスカル・ウォリス検定(Kruskal-Wallis test)は、簡単に言うと、3つ以上のグループのデータが同じ特性を持っているかどうか(言い換えると、サンプル群の中央値に差があるかどうか)を調べるための統計的手法です。これは、通常の分散分析(ANOVA)の代わりに使われる ...
ReadMore

統計検定
2024/2/28
Rでチューキークレーマー法(Tukey‒Kramer法)をやろう
チューキークレーマー法の基本 チューキークレーマー法(Tukey-Kramer method)は、複数のグループ間の平均値の比較に用いられる統計的手法です。この方法は、F統計量を用いない多重比較なので、特に分散分析(ANOVA)を行わなくても検定することができます。チューキークレーマー法は、「どのグループ間に差があるか」を特定するために使われます。また、チューキークレーマー法は、異なるサイズのサンプルにも適用可能です。 統計的背景 多重比較問題: 複数の比較を行うと、誤った結果(第一種の過誤)が生じる確率 ...
ReadMore

統計検定
2024/2/28
ウィルコクソンの符号付順位和検定(Wilcoxon Signed-Rank Test)とは? 実際にRでやってみよう
ウィルコクソンの符号付順位和検定(Wilcoxon Signed-Rank Test)は、統計学において広く使われているノンパラメトリックな検定方法です。この検定は、特にサンプルサイズが小さい場合やデータが正規分布に従わない場合に有効で、対応する2つのサンプル間の中央値の差異が偶然によるものかどうかを評価するために使用されます。以下では、この検定の基本的な概念、手順、適用例、注意点を初学者向けに詳しく解説します。 ウィルコクソンの符号付順位和検定の基本概念とは ウィルコクソンの符号付順位和検定は、2つの関 ...
ReadMore

数学
2025/2/27
偏微分とは?初心者向けにわかりやすく解説!計算方法や応用事例まで
数学や物理、経済学、機械学習の分野では、「偏微分」という概念が頻繁に登場します。 例えば、以下のような場面で偏微分が活用されます。 ✅ 物理学:物体の運動を記述する方程式(速度や加速度)を導く✅ 経済学:利潤最大化やコスト最小化の最適化問題を解く✅ 機械学習:ニューラルネットワークの学習アルゴリズム(勾配降下法)に利用 では、偏微分とは何なのか?どのように計算すればよいのか?本記事では、偏微分の基礎から応用までを詳しく解説 していきます! 1. 偏微分の基礎知識 ...
ReadMore

統計学基礎
2025/2/27
多重共線性とは?統計分析への影響と対策、Rでの検出方法を徹底解説!
統計分析や機械学習において、説明変数(独立変数)同士が強い相関を持つこと は、回帰モデルの推定精度を低下させる可能性があります。 このような状況を 「多重共線性(Multicollinearity)」 と呼びます。 多重共線性が起こると何が問題か? ✅ 回帰係数の推定値が不安定 になり、解釈が難しくなる✅ 統計的な有意性(p値)が正しく評価できなくなる✅ モデルの予測精度が低下 し、新しいデータに対して適用しにくくなる 例えば、以下のようなデータセットを考えます。 ...
ReadMore

回帰分析
2025/2/26
偏回帰分析とは?基本概念から解釈、Rによる実装まで徹底解説!
統計分析において、「ある説明変数が目的変数に与える影響を評価したい」と考えることはよくあります。しかし、多くのデータには 複数の説明変数が同時に影響を及ぼしている ため、単純な単回帰分析では正しい評価ができないことがあります。 そこで活用されるのが 偏回帰分析(Partial Regression Analysis) です。 ✅ 偏回帰分析の主な目的 特定の変数が目的変数に与える影響を、他の変数の影響を除外した上で評価する 多変量データの中で、各説明変数の相対的な寄与度を明確にする 重回帰分 ...
ReadMore

統計学基礎
2025/2/26
ベイズ統計学とは?事前確率と事後確率を用いた推論の基礎からRでの実装まで徹底解説!
統計学において、「新しい情報を得たときに、既存の知識をどのように更新するか?」という問題は非常に重要です。その問題に答えるのがベイズ統計学 です。 ベイズ統計学(Bayesian Statistics) は、事前確率(prior probability)と新しいデータの尤度(likelihood)を組み合わせ、事後確率(posterior probability)を求めることで推論を行います。 例えば、以下のようなケースで活用されています。 ✅ 医療診断:「ある検査で陽性が出た場合、本当に病 ...
ReadMore

R言語
2025/2/26
ベルヌーイ分布とは?確率論の基本から具体例、Rでのシミュレーションまで解説!
確率論や統計学の基礎において、「ある事象が起こるか、起こらないか」を表現するのに便利な分布がベルヌーイ分布です。 例えば、 コインを投げたときに表(1)が出る確率 メールがスパム(1)かそうでない(0)か 機械が正常に作動するか(1)しないか(0) このように、結果が**「成功」または「失敗」の二択** となる確率モデルを扱う際にベルヌーイ分布が使われます。本記事では、以下のポイントを解説します。 ✅ ベルヌーイ分布の基本概念と性質✅ 実際のデータや応用例を用いた説明' ...
ReadMore