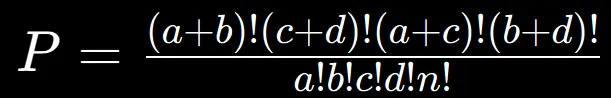こんにちは!統計学に初めて触れる方々へ、今回は「フィッシャーの正確確率検定」についてわかりやすく解説していきます。この名前、ちょっと長くて難しそうですよね。でも、心配しないでください。一緒にゆっくりと学びましょう!
1. フィッシャーの正確確率検定とは?
フィッシャーの正確確率検定は、2x2のクロス表(2行2列の表)におけるカテゴリー間の関連性を検証するための統計的手法です。この検定は、特にサンプルサイズが小さい場合に、行と列の間の関連性(独立性)が偶然によるものかどうかを評価する際に有効です。
フィッシャーの正確確率検定の背景
統計学において、2つのカテゴリー変数間の関連性を評価するための基本的な方法としてカイ二乗検定が知られています。しかし、このカイ二乗検定は、各セルの期待度数が一定以上(通常は5以上)であることを前提としています。サンプルサイズが小さい場合、この条件を満たさないことがよくあり、その結果としてカイ二乗検定の結果が不正確になる恐れがあります。
フィッシャーの正確確率検定は、このような小さいサンプルサイズでも適切に2x2クロス表の関連性を評価できるように設計されています。
どのように動作するのか?
この検定の基本的なアイディアは、観測されたクロス表が得られる確率を計算することです。そして、その確率が非常に低い(例: 5%未満)場合、我々は2つのカテゴリー変数が独立ではないと結論づけることができます。
具体的には、与えられたマージン合計(行合計と列合計)を保持したまま、可能な2x2テーブルのすべての組み合わせを考慮します。観測されたテーブル、またはそれよりもさらに極端なテーブルが偶然によって得られる確率(p値)を計算します。
フィッシャーの正確確率検定の重要性
サンプルサイズが小さいとき、通常のカイ二乗検定を使用すると、Type Iの誤差(偽陽性)のリスクが高まります。フィッシャーの正確確率検定は、このリスクを最小限に抑えるための手段として開発されました。したがって、小さいサンプルサイズのデータに対する信頼性の高い結果を求める場面で非常に役立つツールとなっています。
なぜ「正確」という名前がついているの?
「正確」という言葉の選択の背後には、この検定の数学的なアプローチとその特性に関連する歴史的背景があります。
-
全ての可能性の考慮: フィッシャーの正確確率検定では、2x2のクロス表のすべての可能な組み合わせに基づく確率が計算されます。つまり、我々の観測データが得られる確率だけでなく、それよりも極端なデータの組み合わせが得られる確率も考慮されます。これにより、実際に得られる確率値は「正確」であると言えるのです。
-
カイ二乗検定との対比: カイ二乗検定は大きなサンプルサイズでのアプローチとして開発されました。しかし、サンプルサイズが小さい場合や期待度数が特定の値を下回るセルが存在する場合、カイ二乗検定の結果は不正確になる可能性があります。フィッシャーの正確確率検定は、このような状況でも「正確な」結果を提供する能力を持っています。
-
サンプルサイズの制約: 従来の統計的手法は、特定のサンプルサイズや分布の前提に基づいています。これに対して、フィッシャーの正確確率検定は、小さなサンプルサイズや期待度数が低いセルでも、確度の高い結果を得ることができる特性を持っています。
フィッシャーの正確確率検定の手順
1. 2x2のクロス表の作成
検討している2つのカテゴリカル変数に基づいて2x2のクロス表を作成します。
| カテゴリAのイベント発生 | カテゴリAのイベント非発生 |
| カテゴリBのイベント発生 | a | b |
| カテゴリBのイベント非発生 | c | d |
ここで、a, b, c, dは、それぞれのセルの観測度数です。
2. 確率の計算
観測されたテーブルに対する確率を計算します。この確率は以下の式に基づいています
ここで、nは全体のサンプルサイズ(= a + b + c + d)です。
3. 全ての可能なテーブルに対する確率の計算
観測されたテーブルと同じマージン合計を持つ全ての2x2テーブルの確率を計算します。
4. p値の計算
観測されたテーブルの確率と、それよりも極端なテーブルの確率を合計してp値を得ます。これにより、観測データが偶然によって得られたものである確率を評価します。
5. 結果の解釈
得られたp値を用いて統計的仮説を評価します。一般的に、p値が特定の有意水準(例えば0.05)を下回る場合、2つのカテゴリ変数間には有意な関連性があると結論されます。
4. 実際の例で理解しよう
問題設定
新しい治療法を開発し、その有効性を既存の治療法と比較して評価したいとします。このために、治療を受けた小さなサンプル群の中で、どちらの治療法がより効果的であるかを調査しました。
| 新しい治療法 | 既存の治療法 |
| 効果があった | 5 | 1 |
| 効果がなかった | 2 | 4 |
この表を基に、新しい治療法が既存の治療法よりも効果的であるかどうかをフィッシャーの正確確率検定を使って評価します。
手順
-
上記の表から、各セルの観測度数を取得します。
- a (新しい治療法で効果があった) = 5
- b (既存の治療法で効果があった) = 1
- c (新しい治療法で効果がなかった) = 2
- d (既存の治療法で効果がなかった) = 4
-
これらの値を元に、フィッシャーの正確確率検定の式を用いてp値を計算します。
-
得られたp値を評価します。もしp値が0.05よりも小さければ、新しい治療法と既存の治療法の間には統計的に有意な差があると解釈できます。
結果: この仮想的な例では、具体的なp値は示していませんが、もしp値が0.05より小さければ、新しい治療法が既存の治療法よりも効果的である可能性が高いという結論になります。
まとめ
フィッシャーの正確確率検定は、小さなサンプルサイズの2x2のクロス表のデータに対して、2つのカテゴリーが関連しているかどうかを調べるための便利なツールです。統計学の奥深さを感じることができる検定方法の一つなので、ぜひ覚えておいてくださいね!

統計検定
2025/2/26
スティール・ドゥワス検定とは?多群比較に適した非パラメトリック手法を徹底解説!
統計分析では、複数の群のデータを比較し、それらの間に統計的な差があるかを調べることが頻繁に行われます。一般的な分散分析(ANOVA)では正規性の仮定が求められるため、データが正規分布に従わない場合には、非パラメトリックな手法が有用です。 スティール・ドゥワス検定(Steel-Dwass test) は、そのような多群比較の際に利用できる非パラメトリックな事後検定の一つで、クラスカル・ウォリス検定(Kruskal-Wallis test) などのノンパラメトリック分散分析の後に使用されます。 本記事では、以 ...
ReadMore

統計検定
2025/2/26
フリードマン検定とは?分かりやすく解説!原理・具体例・Rでの実装まで徹底解説
統計学において、データの比較を行う手法は数多く存在します。その中でも、「フリードマン検定」は、対応のある3群以上のデータを比較するための非パラメトリックな方法です。本記事では、フリードマン検定の基本概念から具体例、Rを使った実装までを詳しく解説します。 フリードマン検定は、対応のあるデータに適用されるため、たとえば同じ被験者に対して異なる条件下でのテストを行う場合に有効です。例えば、ある食品メーカーが新しい3種類のレシピを開発し、同じパネリストに試食してもらった場合、それぞれの食品の評価に違いがあるかをフ ...
ReadMore

統計検定
2024/2/28
クラスカルウォリス検定とは? 実際にRでやってみよう
統計学の中でも特に興味深いツールであるクラスカル・ウォリス検定について、より深く掘り下げてみましょう。この検定は、特にサンプルサイズが小さい場合や、データが正規分布に従わない場合に重宝されます。 クラスカル・ウォリス検定とは何か? クラスカル・ウォリス検定(Kruskal-Wallis test)は、簡単に言うと、3つ以上のグループのデータが同じ特性を持っているかどうか(言い換えると、サンプル群の中央値に差があるかどうか)を調べるための統計的手法です。これは、通常の分散分析(ANOVA)の代わりに使われる ...
ReadMore

統計検定
2024/2/28
Rでチューキークレーマー法(Tukey‒Kramer法)をやろう
チューキークレーマー法の基本 チューキークレーマー法(Tukey-Kramer method)は、複数のグループ間の平均値の比較に用いられる統計的手法です。この方法は、F統計量を用いない多重比較なので、特に分散分析(ANOVA)を行わなくても検定することができます。チューキークレーマー法は、「どのグループ間に差があるか」を特定するために使われます。また、チューキークレーマー法は、異なるサイズのサンプルにも適用可能です。 統計的背景 多重比較問題: 複数の比較を行うと、誤った結果(第一種の過誤)が生じる確率 ...
ReadMore

統計検定
2024/2/28
ウィルコクソンの符号付順位和検定(Wilcoxon Signed-Rank Test)とは? 実際にRでやってみよう
ウィルコクソンの符号付順位和検定(Wilcoxon Signed-Rank Test)は、統計学において広く使われているノンパラメトリックな検定方法です。この検定は、特にサンプルサイズが小さい場合やデータが正規分布に従わない場合に有効で、対応する2つのサンプル間の中央値の差異が偶然によるものかどうかを評価するために使用されます。以下では、この検定の基本的な概念、手順、適用例、注意点を初学者向けに詳しく解説します。 ウィルコクソンの符号付順位和検定の基本概念とは ウィルコクソンの符号付順位和検定は、2つの関 ...
ReadMore

特殊なグラフ
2024/4/26
R言語でQQプロットを作成する方法
はじめに QQプロット(Quantile-Quantileプロット)は統計分析で非常に役立つツールです。これを使って、データセットが特定の理論分布に従っているかどうかを視覚的に評価することができます。R言語には、この種のプロットを簡単に作成できる強力なツールが用意されています。この記事では、R言語を使用してQQプロットを作成する基本的なステップを説明します。 必要なパッケージ QQプロットを描くためには、基本的にstatsパッケージが必要ですが、これはRの標準パッケージに含まれているため、特別なインストー ...
ReadMore

グラフのカスタマイズ
2024/4/17
Rでエラーバー付きのグラフを作成する方法
はじめに データの可視化において、エラーバーはデータの変動や不確実性を表現する重要な手段です。R言語を用いたグラフ作成においてエラーバーを追加する方法を学ぶことで、データの解釈をより深く行うことが可能になります。この記事では、基本的なエラーバーの追加方法から、カスタマイズする方法までを段階的に解説します。 エラーバーを含むグラフの重要性 エラーバーは、データ点のばらつきや測定の不確かさを表すのに役立ちます。科学研究や技術報告でよく見られるこの表現方法は、データの信頼性や有効性を視覚的に伝えるために不可欠で ...
ReadMore

グラフのカスタマイズ
2024/4/17
R言語でのグラフ作成:X軸とY軸のスケール比の設定方法
はじめに R言語はデータ分析と可視化に非常に強力なツールです。特にグラフ作成機能は多くのデータサイエンティストや研究者に利用されています。この記事では、R言語でグラフを作成する際にX軸とY軸のスケール比を設定する方法を詳しく解説します。スケール比を調整することで、データの比率や関係性をより正確に表現することが可能になります。 グラフの基本的な作成方法 まず、R言語で基本的なグラフを作成する方法から見ていきましょう。ここでは、plot() 関数を使用してシンプルな散布図を描きます。 # サンプルデータの生成 ...
ReadMore

特殊なグラフ
2024/4/18
R言語でバイオリンプロットを作成する方法:データの分布を視覚化
はじめに バイオリンプロットは箱ひげ図の概念を拡張したもので、データの分布密度も同時に表現できるグラフです。この記事では、R言語を用いてバイオリンプロットを作成する手順を、基本から応用まで丁寧に解説します。 バイオリンプロットとは? バイオリンプロットは、データの確率密度を視覚的に表現する方法の一つで、中央値や四分位数といった統計量だけでなく、データの分布形状も示すことができます。これにより、データの全体的な傾向をより詳細に把握することが可能になります。 Rでバイオリンプロットを作成する Rでは、ggpl ...
ReadMore

グラフのカスタマイズ
2024/4/18
R言語で箱ひげ図に平均値を追加する方法
はじめに 箱ひげ図はデータの分布、特に四分位数や極値を視覚的に表現する強力なツールですが、時には平均値を表示することでデータの理解をさらに深めることができます。この記事では、R言語を使用して箱ひげ図に平均値を追加する方法を解説します。 箱ひげ図とは? 箱ひげ図(Boxplot)は、データの中央値、四分位数、外れ値を表示し、データの分布を要約するのに役立ちます。しかし、平均値もまたデータの中心傾向を理解するのに重要な指標であり、これを箱ひげ図に追加することで、さらに多角的なデータ解析が可能になります。 Rで ...
ReadMore