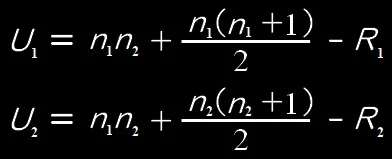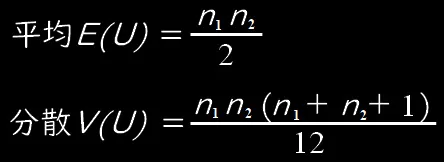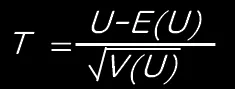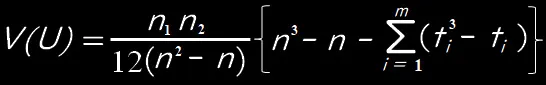RでマンホイットニーのU検定をやろう

マンホイットニーのU検定（またはウィルコクソンの順位和検定とも呼ばれます）は、非パラメトリック統計手法の一つで、二つの独立したグループ間で中央値が異なるかどうかを検定する方法です。この検定は、データが正規分布をしていない場合や、サンプルサイズが小さい場合に特に有効です。

検定の基本ステップ

1.データの準備: 二つの独立したサンプル（グループAとB）を用意します。

2.データのランク付け: 両グループのデータを合わせ、それらに対してランク（順位）を付けます。最も低いデータには1、次に低いデータには2というように順にランクをつけます。同位のデータがある場合（例えば、二つのデータポイントが同じ値を持つ場合）、それらの平均順位を割り当てます。

3.ランクの合計の計算: それぞれのグループのデータポイントのランクの合計を計算します。

4.検定統計量U値の計算: ランクの合計からU値（名前にちなんで記号Tの代わりにUを使います）を計算します。U値は、二つのグループ間でランクがどのように分布しているかを示します。計算式は次のようになります。U $1 $ とU $2 $ $$ のうち小さいほうの値をUとします。

ここで、 $n 1 $ と $n 2 $ はそれぞれのグループのサイズ、 $R 1 とR$ ₂ は各グループのランクの合計です。

注）データ数が大きい場合は検定統計量（T)が

の正規分布に従うことを利用し、

を使って、ｚ検定を行います。

また、同順位がある場合には、V(U)は次式で計算します。

ただし、mは同順位の数、tは同順位の個数（t=1,2,・・・,m)になります。
例えば、順位が2となるもの（2位）が3個と順位が５となるもの（5位）が4個ある場合ではm=2、t₁=3、t₂=4となります。

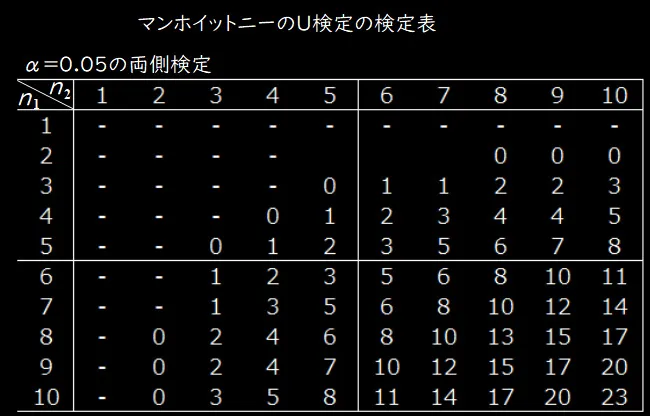
5.統計的意義の判断: 計算されたU値を用いて、統計的に有意な差があるかを判断します。これには、U値の分布表や、大きなサンプルサイズの場合は正規分布の近似を使用します。

6.比較

U値≦棄却限界値の場合、帰無仮説を棄却する
U値＞棄却限界値の場合、帰無仮説を棄却しない
注）U検定では、値の小さい方を検定統計量としており、検定表も検定統計量が0，1，2・・・に対して作られているので、帰無仮説はｚ分布やｔ分布などとは逆に、検定統計量≦棄却限界値の場合に棄却されます。

注意点

マンホイットニーのU検定は中央値の違いを検定しますが、平均値の違いを検定するものではありません。
データに多くの同位値がある場合、検定の精度が低下する可能性があります。
小さなサンプルサイズの場合、検定結果の解釈には慎重さが求められます。

この検定は、データの分布に柔軟で、特に非正規分布のデータに対して強力なツールとなります。そのため、医学、心理学、社会科学などの分野で広く用いられています。

例題を使った解説

新しい教育プログラムの効果の評価

仮定しましょう、ある教育研究者が新しい数学教育プログラムの効果を評価したいと考えています。この研究者は、従来のプログラムを使用している学校（グループA）と、新しいプログラムを採用している学校（グループB）の学生の数学テストスコアを比較することにしました。

データ収集

グループA（従来のプログラム）: 10人の学生のスコアを収集します。例えば、スコアは次のようになります: [70, 75, 80, 65, 90, 85, 78, 82, 88, 76]
グループB（新しいプログラム）: こちらも10人の学生のスコアを収集します。例えば、スコアは次のようになります: [85, 80, 90, 88, 95, 92, 85, 90, 87, 91]

帰無仮説と対立仮説

帰無仮説：両グループの母代表値に差は無い

対立仮説：両グループの母代表値に差がある

データのランク付け

両グループのスコアを合わせて、全体のランクをつけます。例えば、最も低いスコア（65）には1のランク、次に低いスコア（70）には2のランクをつけ、以降同様に進めます。同位のスコアがある場合、それらの平均ランクを割り当てます。

U値の計算

それぞれのグループのランクの合計を計算し、U値を求めます。U値は、あるグループのランクの合計から、そのグループのサイズに関連する量を差し引いて求められます。

計算していくとU=14になるはずです。

統計的意義の判断

計算されたU値を基に、統計的に有意な差があるかどうかを判断します。通常、この判断はU値の分布表または正規分布の近似を用いて行われます。

先ほど表を掲載しましたマンホイットニーのＵ検定の検定表によると、n₁=10、n₂=10の時の限界棄却値は23になります。U＝14＜23なので、帰無仮説は棄却され対立仮説が採用されます。よって、新しい教育プログラムが従来のプログラムと比べて学生の数学スコアに有意な差をもたらすという結論になります。

マンホイットニーのU検定は、特にサンプルサイズが小さく、データが正規分布に従わない場合に有効な手段となります。

例題をR言語を使って解いてみましょう

スクリプトは以下のようになります。

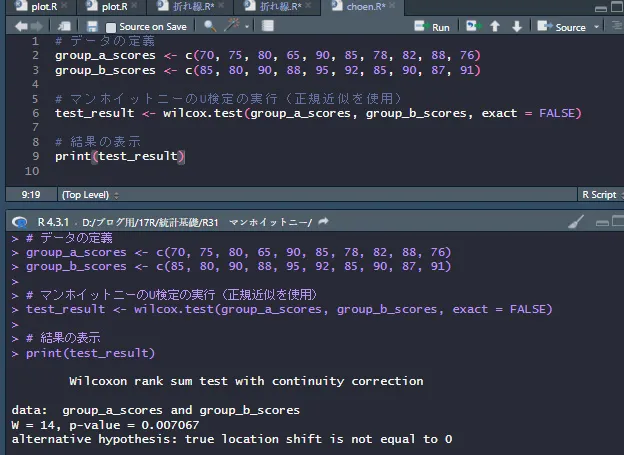
# データの定義
group_a_scores <- c(70, 75, 80, 65, 90, 85, 78, 82, 88, 76)
group_b_scores <- c(85, 80, 90, 88, 95, 92, 85, 90, 87, 91)

# マンホイットニーのU検定の実行（正規近似を使用）
test_result <- wilcox.test(group_a_scores, group_b_scores, exact = FALSE)

# 結果の表示
print(test_result)

スクリプトを実行すると、次のとおりの結果が表示されます。

同じ値のデータ（タイ）がある場合、そのまま計算してしまうと「タイがあるため、正確なp値を計算することができません」という警告が出ます。

RがマンホイットニーのU検定を行った際に、データセット内に多数のタイ（同位値、つまり同じ値を持つデータポイント）が存在する場合に表示されます。

これは、多数のタイが存在すると、標準的なU検定の方法で正確なp値を計算するのが難しいことを意味します。

この問題を解決するために、Rのwilcox.test関数にはexactパラメータがあり、これをFALSEに設定することで、正規近似を使用してp値を計算することができます。ただし、この方法はサンプルサイズが大きい場合に適しています。

計算結果をみると、
W＝１４となっていますが、U＝１４と読み替えてください。
p値は 0.007067 です。p値は帰無仮説（この場合、二つのグループ間で中央値に差がないという仮説）が真である場合に、得られた結果（またはそれ以上に極端な結果）が観測される確率を示します。

一般的に、p値が0.05以下であれば、帰無仮説を棄却し、二つのグループ間に統計的に有意な差があると結論づけます。この場合、p値は0.05よりも小さいため、帰無仮説を棄却します。さきほど、手計算した結果と同じですね。

特殊なグラフ

2024/4/26

R言語でQQプロットを作成する方法

はじめに QQプロット（Quantile-Quantileプロット）は統計分析で非常に役立つツールです。これを使って、データセットが特定の理論分布に従っているかどうかを視覚的に評価することができます。R言語には、この種のプロットを簡単に作成できる強力なツールが用意されています。この記事では、R言語を使用してQQプロットを作成する基本的なステップを説明します。必要なパッケージ QQプロットを描くためには、基本的にstatsパッケージが必要ですが、これはRの標準パッケージに含まれているため、特別なインストー ...

グラフのカスタマイズ

2024/4/17

Rでエラーバー付きのグラフを作成する方法

はじめにデータの可視化において、エラーバーはデータの変動や不確実性を表現する重要な手段です。R言語を用いたグラフ作成においてエラーバーを追加する方法を学ぶことで、データの解釈をより深く行うことが可能になります。この記事では、基本的なエラーバーの追加方法から、カスタマイズする方法までを段階的に解説します。エラーバーを含むグラフの重要性エラーバーは、データ点のばらつきや測定の不確かさを表すのに役立ちます。科学研究や技術報告でよく見られるこの表現方法は、データの信頼性や有効性を視覚的に伝えるために不可欠で ...

グラフのカスタマイズ

2024/4/17

R言語でのグラフ作成：X軸とY軸のスケール比の設定方法

はじめに R言語はデータ分析と可視化に非常に強力なツールです。特にグラフ作成機能は多くのデータサイエンティストや研究者に利用されています。この記事では、R言語でグラフを作成する際にX軸とY軸のスケール比を設定する方法を詳しく解説します。スケール比を調整することで、データの比率や関係性をより正確に表現することが可能になります。グラフの基本的な作成方法まず、R言語で基本的なグラフを作成する方法から見ていきましょう。ここでは、plot() 関数を使用してシンプルな散布図を描きます。 # サンプルデータの生成 ...

特殊なグラフ

2024/4/18

R言語でバイオリンプロットを作成する方法：データの分布を視覚化

はじめにバイオリンプロットは箱ひげ図の概念を拡張したもので、データの分布密度も同時に表現できるグラフです。この記事では、R言語を用いてバイオリンプロットを作成する手順を、基本から応用まで丁寧に解説します。バイオリンプロットとは？バイオリンプロットは、データの確率密度を視覚的に表現する方法の一つで、中央値や四分位数といった統計量だけでなく、データの分布形状も示すことができます。これにより、データの全体的な傾向をより詳細に把握することが可能になります。 Rでバイオリンプロットを作成する Rでは、ggpl ...

グラフのカスタマイズ

2024/4/18

R言語で箱ひげ図に平均値を追加する方法

はじめに箱ひげ図はデータの分布、特に四分位数や極値を視覚的に表現する強力なツールですが、時には平均値を表示することでデータの理解をさらに深めることができます。この記事では、R言語を使用して箱ひげ図に平均値を追加する方法を解説します。箱ひげ図とは？箱ひげ図（Boxplot）は、データの中央値、四分位数、外れ値を表示し、データの分布を要約するのに役立ちます。しかし、平均値もまたデータの中心傾向を理解するのに重要な指標であり、これを箱ひげ図に追加することで、さらに多角的なデータ解析が可能になります。 Rで ...

統計検定

2024/2/28

クラスカルウォリス検定とは？　実際にRでやってみよう

統計学の中でも特に興味深いツールであるクラスカル・ウォリス検定について、より深く掘り下げてみましょう。この検定は、特にサンプルサイズが小さい場合や、データが正規分布に従わない場合に重宝されます。クラスカル・ウォリス検定とは何か？クラスカル・ウォリス検定（Kruskal-Wallis test）は、簡単に言うと、3つ以上のグループのデータが同じ特性を持っているかどうか（言い換えると、サンプル群の中央値に差があるかどうか）を調べるための統計的手法です。これは、通常の分散分析（ANOVA）の代わりに使われる ...

統計検定

2024/2/28

Rでチューキークレーマー法（Tukey‒Kramer法）をやろう

チューキークレーマー法の基本チューキークレーマー法（Tukey-Kramer method）は、複数のグループ間の平均値の比較に用いられる統計的手法です。この方法は、F統計量を用いない多重比較なので、特に分散分析（ANOVA）を行わなくても検定することができます。チューキークレーマー法は、「どのグループ間に差があるか」を特定するために使われます。また、チューキークレーマー法は、異なるサイズのサンプルにも適用可能です。統計的背景多重比較問題: 複数の比較を行うと、誤った結果（第一種の過誤）が生じる確率 ...

統計検定

2024/2/28

ウィルコクソンの符号付順位和検定（Wilcoxon Signed-Rank Test）とは？実際にRでやってみよう

ウィルコクソンの符号付順位和検定（Wilcoxon Signed-Rank Test）は、統計学において広く使われているノンパラメトリックな検定方法です。この検定は、特にサンプルサイズが小さい場合やデータが正規分布に従わない場合に有効で、対応する2つのサンプル間の中央値の差異が偶然によるものかどうかを評価するために使用されます。以下では、この検定の基本的な概念、手順、適用例、注意点を初学者向けに詳しく解説します。ウィルコクソンの符号付順位和検定の基本概念とはウィルコクソンの符号付順位和検定は、2つの関 ...

統計検定

2024/2/28

ブルンナー・ムンチェル検定（Brunner-Munzel Test）とは？実際にRでやってみよう

ブルンナー・ムンチェル検定は、統計学において重要な位置を占める検定方法の一つです。この検定は、特に順序尺度データや不完全なデータに対して有効であり、標準的なt検定やANOVA（分散分析）が適用できない場合に役立ちます。ブルンナー・ムンチェル検定の基本ブルンナー・ムンチェル検定は、非パラメトリックな統計的検定方法の一つです。この検定は、特にデータが正規分布に従わない場合や、サンプルサイズが異なる群間での比較に適しています。順序尺度データ（例：評価が1から5までのスケールで行われる場合）や、不完全なデータ ...

統計検定

2024/2/28

マンホイットニーのU検定とは？　実際にRでやってみよう

マンホイットニーのU検定（またはウィルコクソンの順位和検定とも呼ばれます）は、非パラメトリック統計手法の一つで、二つの独立したグループ間で中央値が異なるかどうかを検定する方法です。この検定は、データが正規分布をしていない場合や、サンプルサイズが小さい場合に特に有効です。検定の基本ステップ 1.データの準備: 二つの独立したサンプル（グループAとB）を用意します。 2.データのランク付け: 両グループのデータを合わせ、それらに対してランク（順位）を付けます。最も低いデータには1、次に低いデータには2という ...

マンホイットニーのU検定とは？　実際にRでやってみよう

検定の基本ステップ

注意点