複数のトレンドを一目で比較することは、データ分析において非常に有用です。本記事では、Rとggplot2を活用して、複数の線を持つ折れ線グラフを作成する方法をステップバイステップで解説します。初心者でも簡単に追随できる内容です。
複数の線を持つ折れ線グラフの描き方
ggplot2を使用して複数の線を持つ折れ線グラフを描くには、いくつかの基本的なステップに従います。
ステップ1: ggplot2のインストールと読み込み
まず、ggplot2パッケージがインストールされていない場合は、インストールします。次に、ライブラリを読み込みます。
install.packages("ggplot2")
library(ggplot2)ステップ2: データの準備
複数の線を持つ折れ線グラフをプロットするためには、まずデータを準備する必要があります。ここでは、例として2つの異なるデータセットを用意します。
# サンプルデータの作成
data1 <- data.frame(
time = seq(1, 10, by = 1),
temperature = c(22, 23, 21, 24, 24, 25, 26, 26, 27, 28),
type = "Type 1"
)
data2 <- data.frame(
time = seq(1, 10, by = 1),
temperature = c(20, 21, 20, 22, 22, 23, 24, 24, 25, 26),
type = "Type 2"
)
data <- rbind(data1, data2)コード解説1
seq(1, 10, by = 1) は、R言語におけるシーケンス生成関数 seq() の一例です。この関数は、指定された開始点、終了点、およびステップ間隔に基づいて数値のシーケンス(連続する数値のリスト)を生成します。
具体的に seq(1, 10, by = 1) は次のことを意味します:
- 開始点は
1 - 終了点は
10 - ステップ間隔は
1
この関数は、1から始まり、1ずつ増加して10で終わる数値のシーケンスを生成します。つまり、結果は 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 という数値のリストになります。
コード解説2
data1 <- data.frame(
time = seq(1, 10, by = 1),
temperature = c(22, 23, 21, 24, 24, 25, 26, 26, 27, 28),
type = "Type 1"
)このコードは、time、temperature、type という3つの列を持つデータフレーム data1 を作成します。ここで、type 列の全ての行に "Type 1" という値が割り当てられます。これにより、データフレーム内の各行は、time と temperature の値に加えて、type として "Type 1" を持つことになります。
ステップ3: 複数の線を持つ折れ線グラフのプロット
次に、ggplot() 関数と geom_line() を使用して複数の線を持つ折れ線グラフをプロットします。
ggplot(data, aes(x = time, y = temperature, color = type)) +
geom_line() +
ggtitle("Temperature Comparison") +
xlab("Time") +
ylab("Temperature")このコードは、time と temperature の値に基づいて折れ線グラフを作成し、type に基づいて異なる色の線を描画します。
ここまでのスクリプトを実行すると次のようになります。
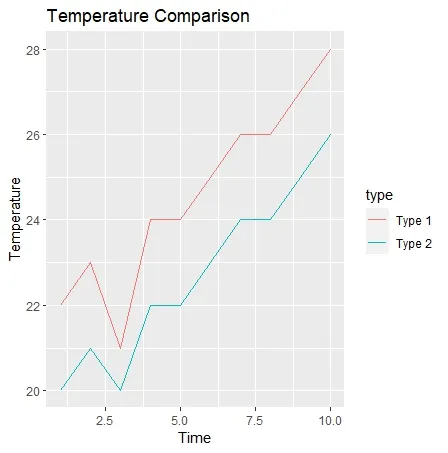
ステップ4: グラフのカスタマイズ
ggplot2では、色の変更、軸のラベル、タイトルなど、グラフの様々な要素をカスタマイズすることができます。
ggplot(data, aes(x = time, y = temperature, color = type)) +
geom_line() +
ggtitle("Temperature Comparison") +
xlab("Time") +
ylab("Temperature") +
theme_minimal() # シンプルなテーマを適用このコードは、折れ線グラフにシンプルなテーマを適用し、見た目を洗練させます。
ここまでのスクリプトを実行すると次のようになります。
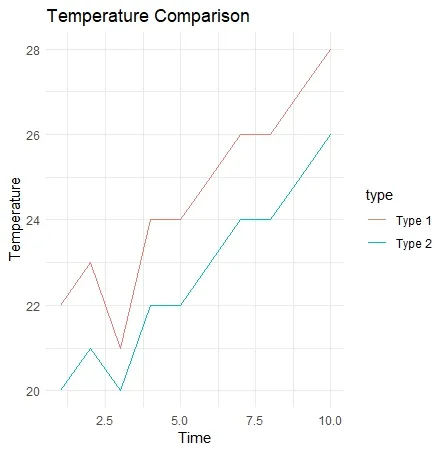
具体例:三種類の折れ線グラフの線の色を指定したい場合
例えば、三種類の折れ線グラフの線の色を指定したい場合のスクリプトは次のようになります。
library(ggplot2)
# サンプルデータの作成
data1 <- data.frame(
time = seq(1, 10, by = 1),
temperature = c(22, 23, 21, 24, 24, 25, 26, 26, 27, 28),
type = "Type 1"
)
data2 <- data.frame(
time = seq(1, 10, by = 1),
temperature = c(20, 21, 20, 22, 22, 23, 24, 24, 25, 26),
type = "Type 2"
)
data3 <- data.frame(
time = seq(1, 10, by = 1),
temperature = c(18, 19, 19, 20, 21, 21, 22, 23, 23, 24),
type = "Type 3"
)
# 三つのデータセットを結合
data <- rbind(data1, data2, data3)
# ggplot2を使用して折れ線グラフを描く
ggplot(data, aes(x = time, y = temperature, color = type)) +
geom_line() +
scale_color_manual(values = c("Type 1" = "blue", "Type 2" = "red", "Type 3" = "green")) + # 手動で色を指定
ggtitle("Temperature Comparison by Type") +
xlab("Time") +
ylab("Temperature")
出力されるグラフは次のようになります。
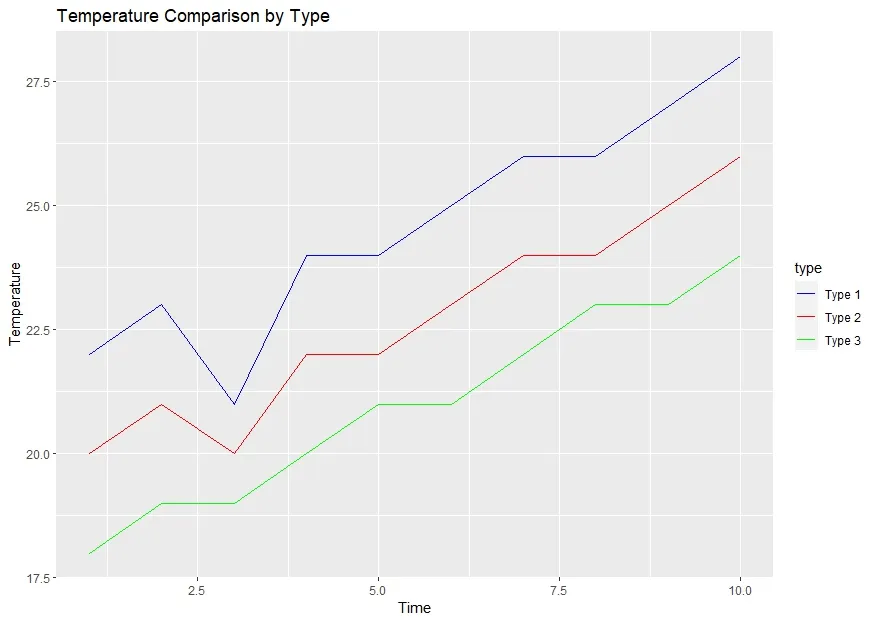
グラフを人によっていろいろ変えたい所は違うと思いますが、やり方の基本は同じなので他の記事にあるやり方を付け足していくだけです。慣れてくると問題なくできるようになります。
まとめ
Rとggplot2を使用して複数の線を持つ折れ線グラフを描く方法は、非常にシンプルで直感的です。この基本をマスターすれば、より複雑なデータセットに対しても同様の手法を適用することができます。データの視覚化は、データの理解を深める重要なステップです。ぜひ、この技術を使って、あなたのデータ分析プロジェクトに新たな洞察を加えてください。











