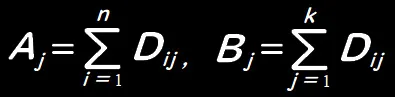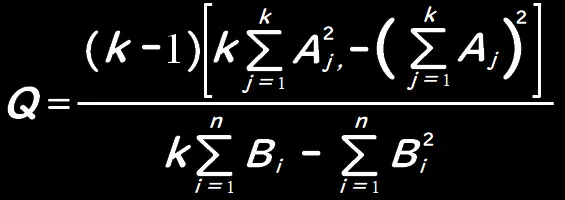コクランのQ検定は統計学において、特にメタ分析で使用される重要な手法です。この検定は、複数の研究結果の間で効果の不均一性があるかどうかを評価するのに使われます。不均一性があるとは、異なる研究から得られた結果のばらつきが、たまたまでは説明できないほど大きいことを意味します。では、具体的な例を交えてこの検定の使用方法を見ていきましょう。
コクランのQ検定の具体的なステップ
1.検定統計量Qを計算
複数の研究から治療効果に関するデータを集めます。たとえば、上の表のようなデータDij(i=1,・・・・,n;j=1,・・・・,k)があるとき、
とおくと、検定統計量Qは次のとおりになります。
Qは自由度f=k-1のχ2分布に従います。
2.カイ二乗分布との比較
計算されたQ統計量をカイ二乗分布の表と比較し、統計的に有意な差があるかを判断します。
3.結論を導き出す
Q<(カイ二乗分布の棄却限界値)の場合、帰無仮説を棄却しない
Q>(カイ二乗分布の棄却限界値)の場合、帰無仮説を棄却
例題
8人の患者に対して、それぞれ治療薬X、Y、Zを投与し治療の効果を調べたところ次の表が得られた。薬の違いによって治療効果の比率に違いがあるかどうかを有意水準0.05で検定する。
| 患者 | X | Y | Z |
| 1 | 0 | 0 | 0 |
| 2 | 1 | 1 | 1 |
| 3 | 1 | 1 | 1 |
| 4 | 1 | 1 | 1 |
| 5 | 0 | 1 | 1 |
| 6 | 0 | 1 | 1 |
| 7 | 0 | 0 | 1 |
| 8 | 0 | 0 | 0 |
解答
帰無仮説:3つの薬の治療効果に差はない
対立仮説:3つの薬の治療効果に差がある
検定統計量Qの計算
処理数 k=3 (j=1,2,3)
患者の数 n=8 (i=1,・・・,8)
ΣAj=A1+A2+A3=3+5+6=14
ΣAj2=A12+A22+A32=32+52+62=70
ΣBj=B1+B2+・・・+B8=0+3+3+3+2+2+1+0=14
ΣBj2=B12+B22+・・・+B82=32+32+32+22+22+12=36
Q=((3-1)×(3×70-142))/(3×14-36)=4.67
棄却域
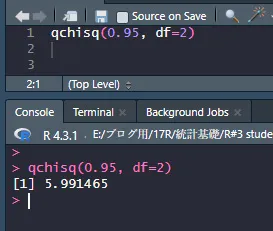
α=0.05で自由度 f=k-1=3-1=2の棄却限界値はχ2乗分布表を使って調べると、5.99146ということが分かります。
またRを使って算出することもできます。次のようにコマンドを記入します。
qchisq(0.95, df=2)
ここで、qchisq() はカイ二乗分布の分位数関数で、第一引数に確率(この場合は 1-有意水準0.05=0.95)、第二引数に自由度(この場合は 2)を指定します。
カイ二乗分布との比較
Q=4.67<5.99なので、帰無仮説を棄却しません。
結論
有意水準5%で、3つの治療薬の効果に違いがあるとはいえない。
R言語でコクランのQ検定のやり方
CochranQTest関数を使用する際の入力方法を詳しく説明します。この関数は、DescToolsパッケージに含まれており、関連する二項変数の群間での差異を検定するために使用されます。まずは、DescToolsパッケージをインストールして読み込む必要があります。
パッケージのインストールと読み込み
install.packages("DescTools")
library(DescTools)
データの準備
CochranQTest関数に入力するデータは、二項的な特性(例:成功=1、失敗=0)を持つ群間での測定値を表す行列形式である必要があります。各行が異なる被験者を、各列が異なる条件や時間点を示すことが一般的です。
先ほどの治療薬のデータを、入力します。
#列データの作成
data <- matrix(c(0, 0, 0,
0, 0, 0,
0, 0, 1,
0, 1, 1,
0, 1, 1,
1, 1, 1,
1, 1, 1,
1, 1, 1),
nrow = 8, byrow = TRUE)
byrow = TRUEというオプションは、R言語で行列を作成する際に使用されるものです。このオプションが指定された場合、与えられたデータは行ごとに(上から下へ)行列に格納されます。デフォルトではbyrow = FALSEになっており、この場合データは列ごとに(左から右へ)行列に格納されます。
検定の実行
データが準備できたら、CochranQTest関数を使って検定を実行します。
CochranQTest(data)
この関数は検定統計量、自由度、p値などの情報を含む結果オブジェクトを返します。p値があなたの設定した有意水準(一般的には0.05)以下であれば、条件間に統計的に有意な差があると解釈できます。
実際にスクリプトを実行した結果をお示しします。
p値は有意水準0.05以上なので、条件間で有意差なしと判断されます。
注意点
CochranQTest関数は、3つ以上の関連する二項変数に適用されます。2つの変数のみの場合は、マクネマー検定を検討してください。- データの形式や検定の前提条件を理解し、適切にデータを準備することが重要です。

特殊なグラフ
2024/4/26
R言語でQQプロットを作成する方法
はじめに QQプロット(Quantile-Quantileプロット)は統計分析で非常に役立つツールです。これを使って、データセットが特定の理論分布に従っているかどうかを視覚的に評価することができます。R言語には、この種のプロットを簡単に作成できる強力なツールが用意されています。この記事では、R言語を使用してQQプロットを作成する基本的なステップを説明します。 必要なパッケージ QQプロットを描くためには、基本的にstatsパッケージが必要ですが、これはRの標準パッケージに含まれているため、特別なインストー ...
ReadMore

グラフのカスタマイズ
2024/4/17
Rでエラーバー付きのグラフを作成する方法
はじめに データの可視化において、エラーバーはデータの変動や不確実性を表現する重要な手段です。R言語を用いたグラフ作成においてエラーバーを追加する方法を学ぶことで、データの解釈をより深く行うことが可能になります。この記事では、基本的なエラーバーの追加方法から、カスタマイズする方法までを段階的に解説します。 エラーバーを含むグラフの重要性 エラーバーは、データ点のばらつきや測定の不確かさを表すのに役立ちます。科学研究や技術報告でよく見られるこの表現方法は、データの信頼性や有効性を視覚的に伝えるために不可欠で ...
ReadMore

グラフのカスタマイズ
2024/4/17
R言語でのグラフ作成:X軸とY軸のスケール比の設定方法
はじめに R言語はデータ分析と可視化に非常に強力なツールです。特にグラフ作成機能は多くのデータサイエンティストや研究者に利用されています。この記事では、R言語でグラフを作成する際にX軸とY軸のスケール比を設定する方法を詳しく解説します。スケール比を調整することで、データの比率や関係性をより正確に表現することが可能になります。 グラフの基本的な作成方法 まず、R言語で基本的なグラフを作成する方法から見ていきましょう。ここでは、plot() 関数を使用してシンプルな散布図を描きます。 # サンプルデータの生成 ...
ReadMore

特殊なグラフ
2024/4/18
R言語でバイオリンプロットを作成する方法:データの分布を視覚化
はじめに バイオリンプロットは箱ひげ図の概念を拡張したもので、データの分布密度も同時に表現できるグラフです。この記事では、R言語を用いてバイオリンプロットを作成する手順を、基本から応用まで丁寧に解説します。 バイオリンプロットとは? バイオリンプロットは、データの確率密度を視覚的に表現する方法の一つで、中央値や四分位数といった統計量だけでなく、データの分布形状も示すことができます。これにより、データの全体的な傾向をより詳細に把握することが可能になります。 Rでバイオリンプロットを作成する Rでは、ggpl ...
ReadMore

グラフのカスタマイズ
2024/4/18
R言語で箱ひげ図に平均値を追加する方法
はじめに 箱ひげ図はデータの分布、特に四分位数や極値を視覚的に表現する強力なツールですが、時には平均値を表示することでデータの理解をさらに深めることができます。この記事では、R言語を使用して箱ひげ図に平均値を追加する方法を解説します。 箱ひげ図とは? 箱ひげ図(Boxplot)は、データの中央値、四分位数、外れ値を表示し、データの分布を要約するのに役立ちます。しかし、平均値もまたデータの中心傾向を理解するのに重要な指標であり、これを箱ひげ図に追加することで、さらに多角的なデータ解析が可能になります。 Rで ...
ReadMore

統計学基礎
2025/2/27
多重共線性とは?統計分析への影響と対策、Rでの検出方法を徹底解説!
統計分析や機械学習において、説明変数(独立変数)同士が強い相関を持つこと は、回帰モデルの推定精度を低下させる可能性があります。 このような状況を 「多重共線性(Multicollinearity)」 と呼びます。 多重共線性が起こると何が問題か? ✅ 回帰係数の推定値が不安定 になり、解釈が難しくなる✅ 統計的な有意性(p値)が正しく評価できなくなる✅ モデルの予測精度が低下 し、新しいデータに対して適用しにくくなる 例えば、以下のようなデータセットを考えます。 ...
ReadMore

回帰分析
2025/2/26
偏回帰分析とは?基本概念から解釈、Rによる実装まで徹底解説!
統計分析において、「ある説明変数が目的変数に与える影響を評価したい」と考えることはよくあります。しかし、多くのデータには 複数の説明変数が同時に影響を及ぼしている ため、単純な単回帰分析では正しい評価ができないことがあります。 そこで活用されるのが 偏回帰分析(Partial Regression Analysis) です。 ✅ 偏回帰分析の主な目的 特定の変数が目的変数に与える影響を、他の変数の影響を除外した上で評価する 多変量データの中で、各説明変数の相対的な寄与度を明確にする 重回帰分 ...
ReadMore

統計学基礎
2025/2/26
ベイズ統計学とは?事前確率と事後確率を用いた推論の基礎からRでの実装まで徹底解説!
統計学において、「新しい情報を得たときに、既存の知識をどのように更新するか?」という問題は非常に重要です。その問題に答えるのがベイズ統計学 です。 ベイズ統計学(Bayesian Statistics) は、事前確率(prior probability)と新しいデータの尤度(likelihood)を組み合わせ、事後確率(posterior probability)を求めることで推論を行います。 例えば、以下のようなケースで活用されています。 ✅ 医療診断:「ある検査で陽性が出た場合、本当に病 ...
ReadMore

統計学
2025/2/26
統計学の歴史③:古代から現代まで、データ分析の進化と発展の軌跡
3. 現代統計学の発展と未来 3-1 コンピュータ革命と統計学 20世紀後半に始まったコンピュータ革命は、統計学の理論と実践に革命的な変化をもたらしました。計算能力の飛躍的向上により、それまで理論上は可能でも実行が困難だった複雑な統計的手法が実用化され、統計学の適用範囲と可能性は大きく拡大しました。 1940年代後半から50年代にかけて開発された初期のコンピュータは、主に軍事目的や科学計算のために使用されていましたが、すぐに統計的計算にも応用されるようになりました。1960年代になると、統計解析専用のソフ ...
ReadMore

統計学
2025/2/26
統計学の歴史②:古代から現代まで、データ分析の進化と発展の軌跡
2. 19世紀~20世紀前半:統計学の黄金期 2-1 統計学の学問的確立 19世紀後半から20世紀初頭にかけて、統計学は独立した学問分野として確立されていきました。この時期、統計学は記述的な段階から分析的・推測的な段階へと発展し、その理論的基盤が大きく強化されました。 この時代の統計学発展の中心となったのが、イギリスの優生学者・統計学者カール・ピアソンです。ゴルトンの研究を引き継いだピアソンは、1901年に「統計的研究のための数学的貢献」を発表し、その中で相関係数(ピアソンの積率相関係数)を定式化しました ...
ReadMore