ブルンナー・ムンチェル検定は、統計学において重要な位置を占める検定方法の一つです。この検定は、特に順序尺度データや不完全なデータに対して有効であり、標準的なt検定やANOVA(分散分析)が適用できない場合に役立ちます。
ブルンナー・ムンチェル検定の基本
ブルンナー・ムンチェル検定は、非パラメトリックな統計的検定方法の一つです。この検定は、特にデータが正規分布に従わない場合や、サンプルサイズが異なる群間での比較に適しています。順序尺度データ(例:評価が1から5までのスケールで行われる場合)や、不完全なデータセットの分析に特に有用です。
検定の原理
ブルンナー・ムンチェル検定は、異なる群間での中央値の差を検証します。この検定は、各群のデータが互いに独立しており、同じ尺度で測定されていることを前提としています。この検定は、通常のt検定やANOVAと異なり、データの分布が非正規であっても、またサンプルサイズが小さくても適用可能です。
検定の手順
- データのランク付け: まず、全てのデータを結合し、小さい順にランク付けします。
- 平均ランクの比較: 次に、各群のデータについて平均ランクを計算し、これらを比較します。
- 統計量の計算: 特定の公式を用いて統計量を計算します。この統計量は、群間の中央値の差に関する情報を提供します。
- p値の計算: 計算された統計量と比較群の数から、p値を計算します。p値は、観測された差が偶然によるものかどうかを判断するために使用されます。
利点と制限
- 利点: 正規分布に依存しない、サンプルサイズが異なる群間の比較に適用可能、順序尺度データに対応。
- 制限: サンプルサイズが非常に小さい場合や、極端に異なる場合は注意が必要です。また、データが独立していることが前提です。
結論
ブルンナー・ムンチェル検定は、従来のパラメトリック検定が適用できない状況でのデータ分析に有効なツールです。この検定を通じて、統計的に有意な結果を得ることができるため、研究者やデータ分析者にとって重要な方法の一つです。
R言語でブルンナー・ムンチェル検定を実施する方法
例題
例えば、ある新しい教育プログラムの効果を評価したいとします。3つの異なる学校でこのプログラムを実施し、その効果を学生の学習意欲の向上という観点で評価します。学習意欲は、非常に低い(1)から非常に高い(5)までの5段階で評価されます。
ここで、各学校の学生の学習意欲のスコアが以下のようになったとします:
- 学校A: [3, 4, 2, 4]
- 学校B: [2, 3, 3, 3, 2]
- 学校C: [4, 4, 5]
このデータを用いて、3つの学校間で学習意欲に有意な差があるかどうかをブルンナー・ムンチェル検定で検証します。
スクリプト
Rでブルンナー・ムンチェル検定を実施するためには、lawstatパッケージに含まれるbrunner.munzel.test関数を使用します。まず、このパッケージをインストールしてロードする必要があります。それから、先ほどの学校の学生の学習意欲のスコアのデータを使用して検定を行います。
以下は、そのためのRスクリプトです。
# lawstatパッケージをインストール(まだインストールしていない場合)
install.packages("lawstat")
# lawstatパッケージをロード
library(lawstat)
# 学校ごとの学習意欲のスコア
school_a <- c(3, 4, 2, 4)
school_b <- c(2, 3, 3, 3, 2)
school_c <- c(4, 4, 5)
# データを結合して、各データポイントに対応するグループのベクトルを作成
scores <- c(school_a, school_b, school_c)
groups <- factor(c(rep("A", length(school_a)),
rep("B", length(school_b)),
rep("C", length(school_c))))
# ブルンナー・ムンチェル検定の実施
result <- brunner.munzel.test(scores, groups)
# 結果の表示
print(result)
このスクリプトでは、まずlawstatパッケージをインストールしてロードします。次に、各学校のスコアをベクトルとして定義し、これらを結合して一つのスコアベクトルを作成します。そして、それぞれのスコアがどの学校に属するかを示すためにグループベクトルを作成します。最後に、brunner.munzel.test関数を使用して検定を行い、結果を表示します。
factorのコマンドについて解説します。
-
rep("A", length(school_a)): この部分は、"A"という文字列をschool_aベクトルの長さ(つまり学校Aのデータポイントの数)と同じ回数だけ繰り返します。結果として、学校Aの各データポイントに対応するだけの"A"の文字列が生成されます。 -
rep("B", length(school_b))とrep("C", length(school_c)): これらは上記と同様の操作を学校Bと学校Cのデータに対して行います。それぞれ"B"と"C"の文字列が、各学校のデータポイントの数に応じて生成されます。 -
c(rep("A", length(school_a)), rep("B", length(school_b)), rep("C", length(school_c))): ここで、上記で生成された各学校のラベルを一つのベクトルに結合します。これにより、全てのデータポイントが、それぞれが属する学校のラベルでマークされるようになります。 -
factor(...): 最後に、この結合されたベクトルをfactor関数に渡すことで、Rで扱う因子(カテゴリカル変数)として定義します。因子は、統計分析においてグループやカテゴリを表すのに適しており、特に検定のような分析では非常に重要です。
結果の解釈
スクリプトを実施すると結果は次のように表示されます。
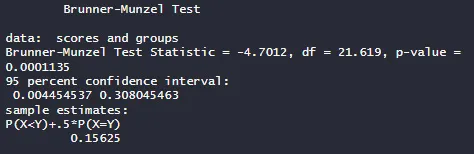
得られたブルンナー・ムンチェル検定の結果を解釈してみましょう。
ブルンナー・ムンチェル検定統計量
- 検定統計量:
-4.7012 - 自由度 (df):
21.619 - p値:
0.0001135
解釈
-
検定統計量: この値は、検定の結果を数値化したものです。この場合、絶対値が大きいため、群間に顕著な差があることを示唆しています。
-
自由度 (df): この値は、検定の計算における自由度を示します。自由度は、データの量と制約の数によって決まり、検定統計量の分布を決定するのに使用されます。
-
p値: この値は、観察された結果(またはそれ以上に極端な結果)が偶然によって発生する確率を示します。一般的に、p値が0.05以下であれば統計的に有意とみなされます。この場合、p値は
0.0001135と非常に小さいため、群間の差が偶然である可能性は非常に低いと考えられます。つまり、統計的に有意な差があると言えます。
信頼区間
- 95%信頼区間:
0.004454537 から 0.308045463
この信頼区間は、群間の差の推定値に関する不確実性の範囲を示しています。この区間は、真の群間差がこの範囲内にあると95%の確信を持って言えることを意味します。
サンプル推定値
- P(X<Y)+.5*P(X=Y):
0.15625
これは、一方の群のスコアがもう一方の群のスコアより小さい確率(P(X<Y))に、スコアが同じである確率(P(X=Y))の半分を加えた値です。この値が0.5から大きく離れている場合、一方の群がもう一方の群よりも統計的に有意に異なることを意味します。この例では、0.15625という値は、一方の群が他の群よりも明らかに異なるスコアを持つことを示唆しています。
結論
この結果は、3つの学校間で学習意欲のスコアにおいて統計的に有意な差が存在することを示しています。p値が非常に低いため、この差が偶然によるものではないと結論づけられます。











